.
Give the general solution to the equation sinx+sin2x+sin3x=0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
sin(x) + sin(2x) + sin(3x) = 0. (1)
Apply the trigonometry formula  =
=  (see any serious textbook in trigonometry or the lessons
- FORMULAS FOR TRIGONOMETRIC FUNCTIONS
- Addition and subtraction of trigonometric functions
in this site) to the first and third addend in the left side of the original equation (1). You will get
(see any serious textbook in trigonometry or the lessons
- FORMULAS FOR TRIGONOMETRIC FUNCTIONS
- Addition and subtraction of trigonometric functions
in this site) to the first and third addend in the left side of the original equation (1). You will get
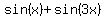 =
= 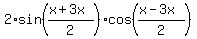 =
= 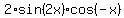 =
= 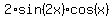 .
Now, the equation (1) takes the form
.
Now, the equation (1) takes the form
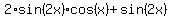 =
=  , or
, or
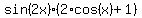 =
=  .
This equation deploys in two independent equations
1. sin(2x) = 0 ---> x =
.
This equation deploys in two independent equations
1. sin(2x) = 0 ---> x =  , x =
, x =  , k = 0, =/-1, +/-2. . . .
2. 2cos(x) + 1 = 0 ---> cos(x) =
, k = 0, =/-1, +/-2. . . .
2. 2cos(x) + 1 = 0 ---> cos(x) =  ---> x =
---> x = 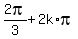 , x =
, x =  , k = 0, =/-1, +/-2. . . .
Answer. The solutions are a) x =
, k = 0, =/-1, +/-2. . . .
Answer. The solutions are a) x =  , x =
, x =  , k = 0, =/-1, +/-2. . . . and
b) x =
, k = 0, =/-1, +/-2. . . . and
b) x = 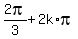 , x =
, x =  , k = 0, =/-1, +/-2. . . .
, k = 0, =/-1, +/-2. . . .
 Plot y = sin(x) + sin(2x) + sin(3x)
Plot y = sin(x) + sin(2x) + sin(3x)
The solution by the other tutor is incorrect.