Question 1068792: John asked Jack how old he is. Jack replied: I am twice as old as you were when I was your age; when you are my age, our ages together will be 63. How old is each of them?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = John's age (in years) = John's age (in years)
 = Jack's age (in years), = Jack's age (in years),
and we assume no tricks, as if both had birthdays on the same day.
Jack uses the phrase "when I was your age," implying that  , ,
but we know that the difference in ages is 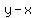 years. years.
So, 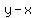 years ago, Jack was Jon's age, and years ago, Jack was Jon's age, and
John was 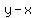 years younger than he is now, so his age was years younger than he is now, so his age was
 . .
Jack says he is twice as old as that, so
 <---> <---> <---> <---> . .
Jack says "when you are my age, our ages together will be 63."
That is in the future, 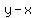 years into the future, years into the future,
since that is the difference in their ages.
At that point,
John's age will be  (Jack's current age), and (Jack's current age), and
Jack's age will be
 . .
The sum of their ages at that point will be
 <---> <---> . .
We have a system of 2 linear equations with 2 variables to solve.
There are many ways to go from initial set of equations to solutions.
Here is the scenic zig-zaggy way:
 --> --> --> --> --> --> --> --> --> --> --> --> --> -->
|
|
|