Question 1068724: The Law of Cosines applies to which cases of oblique triangles?
A.) AAA and SSS
B.) SSS and ASA
C.) SAS and SSS
D.) SAS and SSA
I think it's C or D.
Found 2 solutions by KMST, Edwin McCravy:
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! The law of cosines formula includes
3 side lengths and one angle.
Given 3 of those, you can find the fourth one,
so C and D look promising,
B would not work for ASA because ASA gives only one side length,
and A is ridiculous, because for AAA,
there is no way for any mathematician to guess the side lengths.
So, what about C and D.
Law of shines is easier to apply,
and can be applied whenever you have any 3 measurements,
including one angle and the opposite side.
That is what you have in SSA,
so for SSA you would use law of sines.
So, I vote for  .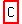
Besides, SSA can be tricky,
not only because you have to be careful not to accidentally spell it backwards,
but because there could be two different triangles with the same SSA.
 If I give you angle A,
side b, and the length of the red sides,
how would you know which red side to choose?
Answer by Edwin McCravy(20060)  (Show Source):
You can put this solution on YOUR website!
It's actually both C and D, although I wouldn't be surprised if your
teacher or book author says the law of cosines cannot be used for SSA.
If they do, they're wrong!
It's not normally used for SSA but it can be used. Below is
proof that the SSA case can be solved completely using the
law of cosines only, and not using the law of sines at all.
The law of cosines can be stated any of these three ways:
1. a² = b² + c² -2bc cos(A)
2. b² = a² + c² -2ac cos(B)
3. c² = a² + b² -2ab cos(C)
Suppose a=8, c=7, C = 60°
Use form 3:
c² = a² + b² -2ab cos(C)
7² = 8² + b² - 2(8)(b)cos(60°)
49 = 64 + b² - 2(8)(b)(1/2)
49 = 64 + b² - 8b
0 = b² - 8b + 15
0 = (b - 5)(b - 3)
b - 5 = 0; b - 3 = 0
b = 5; b = 3
Then for b = 5 use the law of cosines form 1
a² = b² + c² -2bc cos(A)
8² = 5² + 7² -2(5)(7) cos(A)
64 = 25 + 49 - 70cos(A)
64 = 74 - 70cos(A)
-10 = -70cos(A)
1/7 = cos(A)
81.8° = A
Then find the third angle by adding
angle B by adding A and C and subtracting
from 180°
81.8° + 60° = 141.8°
180° - 141.8° = 38.2°
So we solved the SSA case completely by
the law of cosines, without using the law of
sines at all.
This was an ambiguous case and we can solve for
the other solution the same way, using b = 5.
So the law of cosines can be used for the SSA case.
Edwin
|
|
|
