Question 1068471: Please can somebody help me with this please it is due tomorrow!! Please!!
The segment of your coaster ride must have at least 3 relative maxima and/or
minima.The coaster ride starts and ends at ground level.The ride dives below the ground into a tunnel at least once,
1. Create a roller coaster function R(t), where t is measured in seconds and R(t), in feet,
measures the height of the roller coaster at time t. R(t) must meet the minimum
Requirements listed above.
2. Create a sketch of this function using technology.
3. List ALL intervals where your graph is increasing and/or decreasing.
4. What are the average rates of change (average speed) of the roller coaster during each
Descent? Which interval is the ‘scariest’? Why?
5. How long is the entire ride of the roller coaster segment that you have created?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! This problem cones up every year.
You may be able to search this site
(or the internet in general) for ideas.
TIPS:
 In the examples below I used t in minutes, and your problem requests that you use t in seconds. You will have to think on humour own (not a bad idea) because you will not be able to use my work, but the explanations still work. In the examples below I used t in minutes, and your problem requests that you use t in seconds. You will have to think on humour own (not a bad idea) because you will not be able to use my work, but the explanations still work.
For parts 1 and 2:
You cannot be expected to design a realistic roller coaster.
Ideally, I would design one as a piece-wise function,
but a polynomial would do for the expected unrealistic coaster design.
The points at ground level would be zeros of the function,
So, if you want the ride to be 5 minutes, with t in minutes,
you need  and and  . .
That can be achieved by having
 and and 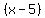 as factors as factors
of your polynomial function.
You also need zeros at the point where you want the ride
to dip below ground, and
to resurface again.
For example,
 for for 
would give you a 5 minute ride that
starts and ends at ground level,
dips below ground between 2 and 3 minutes into the ride,
has a maximum somewhere between 0 and 2 minutes,
a minimum somewhere between 2 and 3 minutes,
and a maximum somewhere between 3 and 5 minutes.
The graph of the function above looks like this:

I gave it a minus sign because
a degree 4 polynomial with a positive leading coefficient
would be positive at its left end,
but would turn negative at its smallest zero,
and I did not want the ride to go underground right after it started.
Use technology (software or a graphing calculator)
to graph your first attempt function,
and change the function,and re-graph until
you are happy with the result.
You can move the middle zeros around to change the shape.
For example, using 2 and 3.5 as the middle zeros,
You get  , and , and
 . .
You can make the ride shorter.
You can have more zeros, and/or a polyomial of higher degree.
You can add zeros at  . .
You can add zeros after the end of the run.
You can n make some zeros double zeros,
as in  . .
 . .
For part 3:
Use your graph Hong,technology to find out the t values
for the maxima and minima.
In between those points,
and between them and the beginning (t=0),
and the end of the ride,
the function/graph is increasing or decreasing.
For example, in the graph above,
the maxima and minima happen at about
 , ,  , and , and  . .
The function
increases in the internal [0, 0.646],
decreases in [0.646,2.624],
increases in [2.624,4.126], and
decreases in [4.126,5].
Part 4:
For the graph above,
in the  minutes minutes
between  and and  , ,
The height goes
from   . .
That is a drop of  feet feet
in  minutes for the first descent. minutes for the first descent.
That is an average rate of
 feet per minute(rounded). feet per minute(rounded).
The other descent goes from  to to  , ,
A drop of  feet in feet in  minutes. minutes.
That is an average rate of
 feet per minute (rounded). feet per minute (rounded).
Obviously the first descent is art a faster rate
(and longer in time, to boot),
so the first descent is scarier.
|
|
|