Question 1067985: Square ABCD has area of 320 square units. Points K, L, M, N are midpoints of the sides of ABCD, P is the point of intersection of KC and BN , and Q is the point of intersection of AM and BN . Find PQ.
Answer by Fombitz(32388)   (Show Source): (Show Source):
You can put this solution on YOUR website!  . .
.
.
.
Set up a coordinate system with B at the origin ( , , ) and s is the length of the side of the square. ) and s is the length of the side of the square.
So then,
N is located at (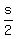 , , ) )
K is located at ( , ,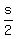 ) )
C is located at ( , , ) )
M is located at ( , ,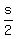 ) )
Find the line BN,



.
.
Find the line KC,



.
.
Find the line AM,


.
.
.
P is the intersection of BN and KC,



and

.
.
.
Q is the intersection of BN and AM,



and

So then the distance PQ is,





In this case,


So,


|
|
|