Question 1067929: Consider matrix A
matrix( 2, 2,
0, 1,
0, 0
)
Show their is not matrix B as Bē = A
Found 2 solutions by t0hierry, ikleyn:
Answer by t0hierry(194)   (Show Source): (Show Source):
You can put this solution on YOUR website! A is a 2 by 2 matrix
(0 1
0 0)
B^2 = A is impossible because the determinant of A is -1. That would mean that det(B)^2 = -1 that is det(B) = +- i
Answer by ikleyn(52800)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution by the other tutor is wrong. Below is the correct solution.
Let A = 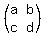 .
Then .
Then 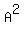 = = 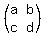 * * 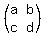 = = 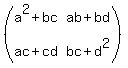 .
If .
If 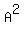 = = 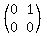 , then
a^2 + bc = 0 (1) as the element (i,j) = (1,1) of the squared matrix;
ab + bd = 1 (2) as the element (i,j) = (1,2) of the squared matrix;
ac + cd = 0 (3) as the element (i,j) = (2,1) of the squared matrix;
bc + d^2 = 0 (4) as the element (i,j) = (2,2) of the squared matrix.
Equation (3) implies that at least one of the two options takes place:
1) c = 0 OR 2) a = -d.
Below I consider every of these two options and derive a contradiction from each of them.
1) if c = 0, then from (1) a^2 = 0; hence, a = 0.
Also, if c = 0, then from (4) d^2 = 0; hence, d = 0.
Then (2) becomes 0 = 1, CONTRADICTION.
2) If a = -d, then again (2) becomes 0 = 1, CONTRADICTION.
These contradictions prove the statement. , then
a^2 + bc = 0 (1) as the element (i,j) = (1,1) of the squared matrix;
ab + bd = 1 (2) as the element (i,j) = (1,2) of the squared matrix;
ac + cd = 0 (3) as the element (i,j) = (2,1) of the squared matrix;
bc + d^2 = 0 (4) as the element (i,j) = (2,2) of the squared matrix.
Equation (3) implies that at least one of the two options takes place:
1) c = 0 OR 2) a = -d.
Below I consider every of these two options and derive a contradiction from each of them.
1) if c = 0, then from (1) a^2 = 0; hence, a = 0.
Also, if c = 0, then from (4) d^2 = 0; hence, d = 0.
Then (2) becomes 0 = 1, CONTRADICTION.
2) If a = -d, then again (2) becomes 0 = 1, CONTRADICTION.
These contradictions prove the statement.
Proved and solved.
|
|
|