Question 1067836: the sum of length, breadth and depth of a cuboid is 19 cm and the length of diagonal is 11 cm. find the surface area of the cuboid.
Found 3 solutions by ikleyn, Alan3354, KMST:
Answer by ikleyn(52771)   (Show Source):
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! d^2 = L^2 + W^2 + H^2 = 11^2 = 121
L^2 + W^2 + H^2 = 121
L + W + H = 19
---------
--> 6 by 6 by 7
SA = 2LW + 2LH + 2WH
SA = 72 + 84 + 84 = 240 sq cm
Other solutions are possible.
-----
After thinking about it, that's the only solution.
Answer by KMST(5328)  (Show Source):
You can put this solution on YOUR website! Let  ,  and  be the length, breadth and depth of the cuboid.
 and
 ---> 
are out clues,
and of course 
 --->
 --->
and yes, there are other options beyond {x,y,z} = {6,6,7} ,
but none with three integers, and the options fall in a narrow range.around
You can make  ,
substitute into
to get an equation of degree 2 in and .
For the equation to have a solution for ,
you need  .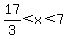
To figure out if there would be another solution with integers,
I searched on line for "Pythagorean quadruples",
sets of 4 whole numbers,  ,
such that  .
The lists are given with the numbers
in such order that  ,
so you only have to the first few
to realize that the only two ending in 11 are
2, 6, 9, 11 and 6, 6, 7, 11 .
|
|
|
