Question 1067802: A stone is dropped from a water tower and its velocity increases at a rate of 32 feet per second squared 2. The stone hits the ground with a velocity of 192 feet per second. What is the formula v(t). What is the domain and range? What does the input variable represent?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  feet per second is the initial velocity, feet per second is the initial velocity,
because the stone was simply let go.
 --> -->  , ,
where 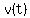 is the downwards velocity in feet per second, is the downwards velocity in feet per second,
and  is the time in seconds since. is the time in seconds since.
 , ,
because the stone's velocity starts as o feet per second,
and increases all the way to 192 feet per second.
The formula for 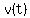 obviously apply to the time the stone is falling, obviously apply to the time the stone is falling,
not before it is dropped, and not after it hits the ground.
so we need to find how long it was falling, by solving
 --> -->  --> -->  . .
 , ,
because the formula/function 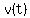 applies only to applies only to
 (time the stone is dropped), (time the stone is dropped),
 (time the stone hits the ground), (time the stone hits the ground),
and all the values of  in between. in between.
|
|
|