Question 1067725: Determine equations for two lines that pass through (1, -5) and are tangent to the graph y= x^2 -2.
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
You can put this solution on YOUR website! 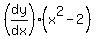
 , slope for any line tangent to y=x^2-2. , slope for any line tangent to y=x^2-2.
 , a line equation , a line equation


 , a line expected to be tangent to y=x^2-2. , a line expected to be tangent to y=x^2-2.
Expression for the parabola, MINUS the expression for the tangent line, should be 0, where the line and parabola intersect. This line is not above the parabola.
 , to solve for finding either of the intersection points. , to solve for finding either of the intersection points.




If x=-1, then y=(-1)^2-2=-1.
Point on parabola, (-1,-1).
If x=3, then y=(3)^2-2=9-2=7.
Point on parabola, (3,7).
The Two Possible Lines Tangent to y=x^2-2, and containing (1,-5):
-
Line containing (1,-5) and (-1,-1).
slope  ; ;
Equation starting point-slope form,

-
Line containing (1,-5) and (3,7).
slope  ; ;
Equation,

|
|
|