SOLUTION: √a^2+b^2=613 where a, b are positive integers. Find a+b

Algebra ->  Square-cubic-other-roots -> SOLUTION: √a^2+b^2=613 where a, b are positive integers. Find a+b      Log On


   

Question 1067650: √a^2+b^2=613 where a, b are positive integers.
Find a+b
Answer by Edwin McCravy(20064) About Me  (Show Source):
You can put this solution on YOUR website!
sqrt%28a%5E2%2Bb%5E2%29%22%22=%22%22613
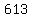
a² + b² = 613

We see if (a,b,613) is a Pythagorean triple
 
let b = 613-k

a² + (613-k)² = 613²

a² + 613² -1226k + k² = 613²

a² - 1226k + k² = 0

We notice that sqrt%281226%29=%2235.01142...%22

So the largest square not exceeding 1226 is 35² = 1225

So we write 1226 = 35² + 1

a² - (35²+1)k + k² = 0

a² = (35²+1)k - k² 

a² = 35²k + k - k²

We see that if k=1 the right side becomes 352

Therefore k=1, and b = 613-k = 613-1 = 612, and a=35

Therefore (a,b,613) = (35,612,613) is a Pythagorean triple.

Thus a+b = 35+612 = 647

Edwin