Question 1067594: John is twice as old as Jane was when he was as old as she is now. The sum of their age is 63. How old is John and Jane
Found 2 solutions by MathTherapy, ikleyn:
Answer by MathTherapy(10551)   (Show Source): (Show Source):
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
John is twice as old as Jane was when he was as old as she is now. The sum of their age is 63. How old is John and Jane
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let x be the John's present age and y be the Jane's present age.
When John was as old as Jane is now ? - Answer: (x-y) years ago.
What was Jane's age then? - Answer: y - (x-y) years, or, which is the same, 2y - x was Jane's age then.
The condition says:
x = 2 *(2y-x), or
x= 4y - 2x, or
3x = 4y. (1)
The second equation is
x + y = 63. (2)
From (2), express x = 63-y and substitute it into (2), replacing x. You will get
3*(63-y) = 4y, or
189 - 3y = 4y ---> 189 = 7y ---> y = 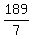 = 27.
Answer. Jane is 27 years old. John is = 27.
Answer. Jane is 27 years old. John is 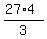 = 36 years old. = 36 years old.
Solved.
For similar solved problems see the lesson
- Really intricate age word problem
in this site.
There is a bunch of lessons on age word problems
- Age problems and their solutions
- A fresh formulation of a traditional age problem
- Really intricate age word problem (*)
- Selected age word problems from the archive
- Age problem for the day of April, 1
- OVERVIEW of lessons on age problems
in this site.
Read them and become an expert in solving age problems.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Age word problems".
|
|
|