SOLUTION: slove the equation over the interval [0,360] or [0,2pi] Sin(X)+Sin(3X)+Sin(5X)=0

The word is "solve", not "slove" :)



Write X as 3X-2X and 5X as 3X+2X



Then use the formulas for sin(A-B) and sin(A+B).
Some terms will cancel.  Then you'll be able to factor 
out sin(3X), and solve.

If you have trouble, tell me about it in the thank-you
not form below and I'll get back to you by email.  I
do not charge any money ever.

Edwin

Sin(X) + Sin(3X) + Sin(5X) = 0.              (1)


Using the Trigonometry formula   ,                    (*)

you can transform    Sin(X) + Sin(5X) =  = .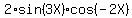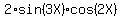


Then the left side of the given equation takes the form 

Sin(X) + Sin(3X) + Sin(5X) =  +  = ,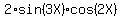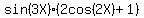

and the equation (1) takes the form 
 
  =  0.                      (2)


Equation (2) deploys in two independent equations:


1)  sin(3X) = 0,  which in the given interval has the solutions  X = 0, , , , , and .


2)  2*cos(2x) + 1 = 0,  which is the same as  cos(2X) = .

    In the given interval the last equation has the solutions

    X = ,  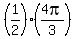,  ,  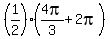,    or, which is the same,

    X = ,  ,    and  .


Answer.  The solutions of the equation (1) in the interval [,)  are  X = 0, , , , , and .