SOLUTION: Please help me with this word problem. The index of refraction {{{ n }}} of a transparent material is the ratio of the speed of light in a vacuum to the speed of light in the ma

Algebra ->  Customizable Word Problem Solvers  -> Misc -> SOLUTION: Please help me with this word problem. The index of refraction {{{ n }}} of a transparent material is the ratio of the speed of light in a vacuum to the speed of light in the ma      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1067578: Please help me with this word problem.
The index of refraction +n+ of a transparent material is the ratio of the speed of light in a vacuum to the speed of light in the material. For the triangular prism in the picture, n = 1.5 and a = 60°. Identify the angle θ for the glass prism if ( see image linked below ) thanks a bunch.
image: https://s28.postimg.org/q8pbxbknx/word_problem.png
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The picture:
n=sin%28theta%2F2%2Balpha%2F2%29%2Fsin%28theta%2F2%29
alpha=60%5Eo= prism angle crossed by the light
alpha%2F2=60%5Eo%2F2=30%5Eo
theta= angle of deviation of the light as it goes through the prism
sin%28alpha%2F2%29=sin%2830%5Eo%29=1%2F2=0.5
cos%28alpha%2F2%29=cos%2830%5Eo%29=sqrt%283%29%2F2=0.5sqrt%283%29

To calculate 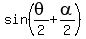sin%28theta%2F2%2Balpha%2F2%29 we need the trigonometric identity formula for a sum of angles:
sin%28A%2BB%29=sin%28A%29%2Acos%28B%29%2Bcos%28A%29%2Asin%28B%29 .


So substituting the expression above,
and the value 1.5 for n
in the formula for refractive index, we get
.
Multiplying both sides of the equal sign times 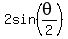2sin%28theta%2F2%29,
we get the equivalent equation
3sin%28theta%2F2%29=sqrt%283%29%2Asin%28theta%2F2%29%2Bcos%28theta%2F2%29
Now, dividing both sides of the equation by 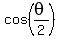cos%28theta%2F2%29 ,
we get the equivalent equation
,
which simplifies to
3tan%28theta%2F2%29=sqrt%283%29%2Atan%28theta%2F2%29%2B1 ,
so
3tan%28theta%2F2%29-sqrt%283%29%2Atan%28theta%2F2%29=1 --> %283-sqrt%283%29%29%2Atan%28theta%2F2%29=1 --> tan%28theta%2F2%29=1%2F%283-sqrt%283%29%29
From
tan%28theta%2F2%29=1%2F%283-sqrt%283%29%29 , or the more elegantly written equivalent
tan%28theta%2F2%29=%283%2Bsqrt%283%29%29%2F6 ,
we can calculate an approximate value for 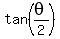tan%28theta%2F2%29 ,
for which your calculator would give you an approximate value for 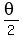theta%2F2 ,
which can be used to calculate an approximate value for theta .
The approximate values would be:
tan%28theta%2F2%29=0.788675 , theta%2F2=38.26%5Eo ,
and highlight%28theta=76.52%5Eo%29 .

An exact value would have to be expressed as an inverse tangent function
theta=2%2Atan%5E%28-1%29%28%283%2Bsqrt%283%29%29%2F6%29 ,
or if you use the double angle trigonometric identity to calculate that tan%28theta%29=%2830%2B14sqrt%283%29%29%2F13 ,
theta=tan%5E%28-1%29%28%2830%2B14sqrt%283%29%29%2F13%29 .
Hopefully no instructor would make you go through all that trouble.