Question 1067383: Two workers and B together could finish a work in 8 days. They worked together for 6 days and A left the work. The remaining work was completed by B alone in 6 days. How many days would each take to complete the work individually ?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! What we have to find is
 = number of days that it would take worker A to complete the job by himself (or herself), = number of days that it would take worker A to complete the job by himself (or herself),
and
 = number of days needed for B to complete the job working alone. = number of days needed for B to complete the job working alone.
In one day of work, the fraction of the job that
A would complete is 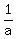 , ,
and the fraction of the job B would complete
is  . .
Working together, they would complete
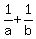 of the job each day, of the job each day,
and that would be  of the job. of the job.
(You could also say that
 ), ),
but either way, you end up with
 . .
 is the fraction of the job is the fraction of the job
that A and B complete, working together,
during the first 6 days.
 is the fraction of the whole job is the fraction of the whole job
that B does all alone, during the next 6 days.
After that, the fraction of the job that has been completed is
 or or  . .
We solve that to find  : :
Multiplying both sides of the equal sign times 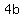
we get the equivalent equation


 . .
Now, substituting the value for 
into  , ,
we get  , ,
which we solve for  . .
First, we multiply both sides of the equal sign
times  to get the equivalent equation to get the equivalent equation





 . .
|
|
|