SOLUTION: when a bus travels a certain route at an average speed of the40km/h it arrives one hour late at its destination, and when it averages48km/h it arrives one hour early. Q1;What is t

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: when a bus travels a certain route at an average speed of the40km/h it arrives one hour late at its destination, and when it averages48km/h it arrives one hour early. Q1;What is t      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1066378: when a bus travels a certain route at an average speed of the40km/h it arrives one hour late at its destination, and when it averages48km/h it arrives one hour early.
Q1;What is the length of the journey?
Q2: How fast should the bus travel in order to arrive on thetime at its destination？
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620) About Me  (Show Source):
You can put this solution on YOUR website!
t, normal expected time
d, one-way trip distance


                    SPEED      TIME       DISTANCE

LATE                40         t+1         d

EARLY               48         t-1         d


Solve this system:
system%2840%28t%2B1%29=d%2C48%28t-1%29=d%29


-
40%28t%2B1%29=48%28t-1%29
5%28t%2B1%29=6%28t-1%29
5t%2B5=6t-6
highlight%28t=11%29-------normally expected time

Q1:
Find d.
40%28t%2B1%29=d
40%2811%2B1%29
40%2A12
highlight%28480%2Akilometers%29

Q2:
What should be the expected speed for the bus if the 480 km trip took 11 hours?
r%2A11=480
r=480%2F11
r=44%28kilometer%2Fhour%29

Answer by ikleyn(52814) About Me  (Show Source):
You can put this solution on YOUR website!
.
when a bus travels a certain route at an average speed of 40 km/h it arrives one hour late at its destination,
and when it averages 48 km/h it arrives one hour early.
Q1;What is the length of the journey?
Q2: How fast should the bus travel in order to arrive on the time at its destination？
~~~~~~~~~~~~~~~~~~~~~~ 

1.  Let D be the length of the journey.

    Then the time of traveling at the speed of 40 km/h is D%2F40 hours, 

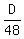    and the time of traveling at the speed of 48 km/h is D%2F48 hours. 

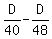    According to the condition, the difference D%2F40+-+D%2F48 is 2 hours.
    It gives an equation

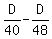    D%2F40+-+D%2F48 = 2.

    To solve it, multiply both sides by 40*48. You will get

    48D - 40D = 2*40*48  --->  8D = 2*40*48  --->  D = 2*40*6 = 840.

    So, the distance is 840 kilometers, and the first question is answered.



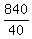2.  Next, the travel time at the speed of 40 km/h is 840%2F40 = 21 hours.

    Hence, the regular/normal/scheduled time is 21 - 1 = 20 hours,  and so

    the regular/normal/scheduled speed is 840/20 = 44 km/h.

Solved.


Similar problem was solved in the lesson
    - How far do you live from school?
in this site.


Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lesson is the part of this textbook under the section "Word problems", the topic "Travel and Distance problems".