|
Question 1066283: Hello! I hope you're having a good day. I'm not quite sure how to write out matrices on here, so I'm going to try my best.
The question is "Evaluate [4 0 7] 3
4
6
Note that the 346 is up and down and has brackets around it.
Possible answers are:
1. [56]
2. [54 1]
3. [54]
4. Does not exist
Thanks so much for your help!
Found 2 solutions by swincher4391, KMST:
Answer by swincher4391(1107)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a good example of matrix multiplication. And it is usually made more complicated than it actually is. Let's forget about what is in the brackets right now and only focus on the dimensions.
Let's let A be the first matrix and it is a 1x3 matrix.
Similarly let's let B be the 2nd matrix and it is a 3x1 matrix.
So compare 1x3 to 3 x 1. The only way for matrix multiplication to work out is if the inside dimensions are exactly the same. In this case 3 = 3, so matrix multiplication is applicable. The dimensions of the result are the outside two numbers. So the answer is going to be a 1x1. This already eliminates the middle choice. But let's be exact here.
A 1x1 matrix is not a very good teaching moment, but take the possible cells that exist in a 1x1 matrix.
The only cell that exists is (1,1). Let's call a11.
a11 can be found by doing a dot product of the 1st row of A and the 1st column of B.
So a11 = (4x3) + (0*4) + (7*6) = 12 + 0 + 42 = 54
So the resulting matrix is [54].
Let me do a slightly harder example since this one was so simple.
You do not have to keep reading, but this next part might help.
------------------------------------------
Let's say we have A = [1 2] and B = [2 1 3]
...........................................3 4..................4 3 1
A x B will work because A is 2x2 and B is 2x3 so the resulting matrix is a 2x3.
The cells in a 2x3 are
a11 a12 a13
a21 a22 a23
a13 for instance is the dot product of the 1st row and 3rd column.
a13 = (1*3) + (2*1) = 5
a21 is the dot product of the 2nd row and 1st column
a21 = (3*2)+(4*4) = 22
See how that works? Let me know if you have any questions at swincher4391@yahoo.com
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! To write algebra in this website,
you wrap whatever you want to write in triple curly brackets,
so 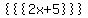 displays as displays as  . .
Matrices are a bit more complicated.
You can get big curved brackets around them by his just typing them,
but to get the numbers in the proper positions
you write "matrix(" followed by numbers, separated by commas:
the number of rows,
the number of columns, and
all the numbers in the matris,in order,
and a ")" to indicate the end of the matrix.
For example, for 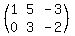 , ,
I have to write (matrix(2,3,1,5,-3,0,3,-2)) wrapped in triple curly brackets.
|
|
|
| |