SOLUTION: Find 3 numbers in the geometrical progression whose sum is 28 and whose product is 512

Let the middle term be "x" and the common ratio be r.

Then the first of the three terms is , and the third term is .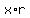


The product of the three terms i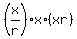s  = .

Thus  = 512, which implies x = 8.

So, you just found the middle term. It is 8.


Then the sum of the three terms is 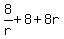 = 28, which gives you an equation

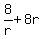 = 28 - 8,   or  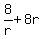 = 28 - 8 = 20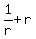,   or    = ,   or 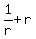  =  = 2.5

which has the roots  r = 2  and/or  r= .


Thus the progression is  {4, 8, 16}   or   {16, 8, 4}.