Question 1065976: Given that theta is an acute angle and sin(theta) = 17/37, find the exact value of sec(theta)
Use the exact values for the sine and cosine of both pi/4 and 2pi/3, and the angle sum identity for cosine, fine the exact value of cos(11pi/12)
use the exact value of cos(11pi/6) and the half-angle identity for sine to find the exact value of sin(11pi/12)
---
I believe to do this question I need to find which quadrants the angles lie in, but beyond that I am just not sure what to do!
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given that  is an acute angle and is an acute angle and  , find the exact value of sec(theta) , find the exact value of sec(theta)
THE SEVENTH GRADER'S POINT OF VIEW:
If  is an acute angle, it could be an angle in a right triangle, and is an acute angle, it could be an angle in a right triangle, and
 can be seen as a trigonometric ratio, can be seen as a trigonometric ratio,
relating the lengths of the hypotenuse and opposite side in a right triangle:
 . With that point of view you do not need to know about quadrants, . With that point of view you do not need to know about quadrants,
or about trigonometric functions.
Then you would find the length of the missing side using the Pythagorean theorem:
 --> -->  --> -->  --> -->  --> -->  . .
Then you would find  as the ratio (adjacent side)/hypotenuse: as the ratio (adjacent side)/hypotenuse:
 (rounded). (rounded).
THE HIGH SCHOOLER'S POINT OF VIEW:
When we need to extend the definitions of trigonometric ratios to larger angles, measuring  or more, which cannot be part of a right triangle, or more, which cannot be part of a right triangle,
we start talking about quadrants and trigonometric functions.
At that point we say that
if  is an acute angle, it si in the first quadrant, is an acute angle, it si in the first quadrant,
where 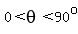 or or  , ,
and all trigonometric functions are positive.
Then, we use  and and 
to find  : :






 (rounded). (rounded).
THE SECOND QUESTION:
That question is beyond the 7th grade math.
At this point in his/her studies,
a student should be resigned to the fact that radians are here to stay,
because degrees are for people whose career options will be limited.
If you are there, you know that a right angle measures  , ,
 , ,
 , ,
 , and , and
 . .
For the rest, you should be allowed to look up the formulas.
If your life is such that you need to look up those formulas often,
you will eventually remember them.
I just search online for "trig identities" and trust Wikipedia.
It says that
 , ,

 , and , and  . .
That is all I need.
I remember the exact values of the trigonometric functions for
 and and  , because those are the angles in , because those are the angles in
the half of a square cut along the diagonal,
and an equilateral triangle:
 ---> ---> 
 <--- <--- 
Now,  : :  , so , so  . .
Now, we can use the exact values for the sine and cosine of both  and and  , ,
and the angle sum identity for cosine, 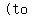  the exact value of the exact value of 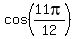
 , ,
so applying the sum identity for cosine

As for using the exact value of 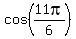 and the half-angle identity for sine to find the exact value of and the half-angle identity for sine to find the exact value of 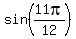
,
we would have to figure out how to find 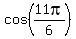 first. first.
And, why would we do that, instead of using the already found value of 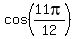 , ,
and the trigonometric identity  ? ?
Well, It is not that hard.
 , so , so 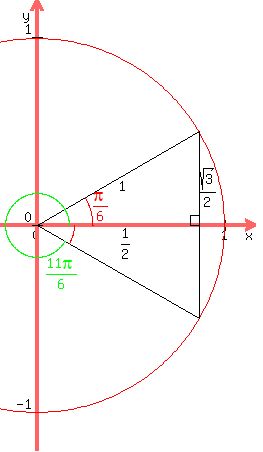 , and we see that , and we see that

Using that, and the half-angle identity for sine,  , ,
 , ,
and since  was almost a full turn, almost at the far end of the fourth quadrant, was almost a full turn, almost at the far end of the fourth quadrant,
we know that half of that, 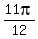 , would be almost, , would be almost,
almost at the end of the second quadrant.
We also know that in the second quadrant sine is positive, and cosine is negative.
So,  . .
|
|
|