f∘g(x) is read "f of (g of x)".
If means the same as 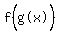 To get it, substitute what g(x) equals, for x in what
f(x) equals. Then simplify.
We start with f(x)
To get it, substitute what g(x) equals, for x in what
f(x) equals. Then simplify.
We start with f(x)
 Then we take what g(x) equals, which is (4x+9), and
substitute it for x in
Then we take what g(x) equals, which is (4x+9), and
substitute it for x in 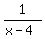 , like this:
, like this: 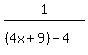 So we have:
f∘g(x) =
So we have:
f∘g(x) = 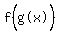


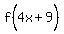

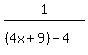 Then we simplify
f∘g(x) =
Then we simplify
f∘g(x) = 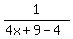 f∘g(x) =
f∘g(x) = 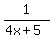 That's the answer.
To find f∘g(5), we merely substitute 5 for x
f∘g(5) =
That's the answer.
To find f∘g(5), we merely substitute 5 for x
f∘g(5) = 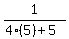 and simplify
f∘g(5) =
and simplify
f∘g(5) = 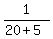 f∘g(5) =
f∘g(5) =  Be sure to watch this youtube video:
https://www.youtube.com/watch?v=S4AEZElTPDo
Edwin
Be sure to watch this youtube video:
https://www.youtube.com/watch?v=S4AEZElTPDo
Edwin