This depends on whether you are still in algebra or in calculus.
I'll do it both ways:
1. Using calculus:
By implicit differentiation:
We set 
equal to 0
, substituting:
Answer, since the + gives the larger value,
the maximum point is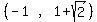 
-------------------------------
2. If you're in algebra,
Swap the middle two terms to get like lettered terms together:
Add 3 to both sides:
Factor 4 out of the first two terms:
Complete the square inside the parentheses:
Add +1 inside the parentheses and add +4*1 to the right side
since 4 times what is added inside the parentheses is added
to the left side and must also be added to the right side.
Complete the square on the y's:
Add +1 to both sides:
Factor the two trinomials, which are perfect squares, and
write them as the squares of binomials, combine numers
on the right side:
Divide through by 8
Compare to the standard equation for an ellipse:
since a > b
center (h,k) = (-1,1), 
, 
Graph:
The highest point on the ellipse is the upper vertex, which has the
same x-coordinate as the center, which is -1,
The y-coordinate of the upper vertex, which is 
units
above the center, which has y-coordinate 1, so we add to
1 and get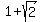 
.
Thus the highest point on the ellipse is:
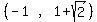Edwin
