Question 1065217: Flying against the wind, a jet travels 5670mi in 7 hours. Flying with the wind, the same jet travels 11,790mi in 9 hours. What is the rate of the jet in still air and what is the rate of the wind?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618)   (Show Source):
You can put this solution on YOUR website! RT=D, constant travel rate rule for rate R, time T, distance D.
r, speed in absence of wind
w, speed of wind
SPEED TIME DISTANCE
WITHWIND r+w 9 11790
AGAINST r-w 7 5670
Answer by ikleyn(52795)  (Show Source):
You can put this solution on YOUR website! .
Flying against the wind, a jet travels 5670 mi in 7 hours. Flying with the wind, the same jet travels 11,790 mi in 9 hours.
What is the rate of the jet in still air and what is the rate of the wind?
~~~~~~~~~~~~~~~~~~~~~~~~
Let u be the speed of the plane at no wind (in mph),
and "v" be the speed of the wind.
Then
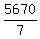 = u - v (1) (speed flying with the wind)
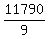 = u + v (2) (speed flying against the wind)
Simplify:
u - v = 810, (1')
u + v = 1310. (2')
Add the two equations (1') and (2'). You will get
2u = 2120 ----> u =  = 1060 mph.
Then from (2') v = 1310 - u = 1310 - 1060 = 250 mph.
Thus the formal answer is: the speed of the plane is 1060 mph, the speed of wind is 250 mph.
Now, the speed of wind of 250 mph is more that a strongest hurricane,
so I don't know who invented this problem.
As well as I don't know for whom I solved it and for what.
Usually I have good advises for people who come to the forum with similar problems,
but in this case, I don't know what to do and how to communicate with them.
|
|
|
