Question 1065154: A small movie theater sells tickets for $15 at this price the theater sells 200 tickets every show the owners know in past years that they will sell eight more tickets per show for each price decrease of $0.50 what function can be used to model the owners earnings if x represents price decrease in dollars
What lower price would let the owners earn the same amount of money they are now
What should the owners charge per ticket to earn the maximum amount of money
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A small movie theater sells tickets for $15 at this price the theater sells 200 tickets every show the owners know in past years
that they will sell eight more tickets per show for each price decrease of $0.50
1. what function can be used to model the owners earnings if x represents price decrease in dollars
2. What lower price would let the owners earn the same amount of money they are now
3. What should the owners charge per ticket to earn the maximum amount of money
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
1. N(x) = 200 + 16x, where x is the price decrease in dollars, N(x) is the number of viewers.
2. To answer the second question, solve the equation
N(x)*(15-x) = 15*200, or, which is the same
(200+16x)*(15-x) = 3000.
 Plots y = (200+16x)*(15-x) and y = 3000
From the plot, you can see that the second solution is the price decrease of $2.50, which gives the ticket price of $12.50,
the number of viewers of 240 and the total amount of money the same $15*200 = $3000.
3. To answer the third question, you need to find the maximum of the quadratic function
q(x) = (200+16x)*(15-x) = -16x^2 + 40x + 3000.
The maximum is achieved at x =
Plots y = (200+16x)*(15-x) and y = 3000
From the plot, you can see that the second solution is the price decrease of $2.50, which gives the ticket price of $12.50,
the number of viewers of 240 and the total amount of money the same $15*200 = $3000.
3. To answer the third question, you need to find the maximum of the quadratic function
q(x) = (200+16x)*(15-x) = -16x^2 + 40x + 3000.
The maximum is achieved at x =  = = 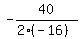 = = 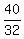 = $1.25.
So, the optimal price decrease is $1.25.
The optimal price for a ticket is $13.75
It provides 220 viewers and the total money amount of 220*$13.75 = $3025.00. = $1.25.
So, the optimal price decrease is $1.25.
The optimal price for a ticket is $13.75
It provides 220 viewers and the total money amount of 220*$13.75 = $3025.00.
To be fully educated in solution of similar problems, see my other lessons in this site on finding the maximum/minimum of a quadratic function
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
- Using quadratic functions to solve problems on maximizing revenue/profit (*)
- OVERVIEW of lessons on finding the maximum/minimum of a quadratic function
Pay a special attention to the lesson marked by (*) in the list.
It contains other similar problems with detailed solutions.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
|
|
|