Question 1064963: Find the greatest 4 digit number with exactly 3 factors.
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! I did this one recently.
#1064533
------------
I'm not sure about the other tutor's answer.
1 is not usually considered when factoring.
If 1 is accepted as a factor, then 9409 can be 1*1*1*1*97*97.
And, if 1 is allowed --> 1*13*769 = 9997
If 1 is not allowed ---> 2*19*263 = 9994
=============================================================
---
If using the same factor more than once is allowed, then
then 3*3*11*101 is the solution.
----------------
But, the author of the problem should have specified whether or not to use 1 as a factor.
====================
It's a useless problem, nothing to be learned from it.
9999 9998 9997 9996 9995 9994 9993 9992 9991 9990
2 4999.50 4999.00 4998.50 4998.00 4997.50 4997.00 4996.50 4996.00 4995.50 4995.00
3 3333.00 3332.67 3332.33 3332.00 3331.67 3331.33 3331.00 3330.67 3330.33 3330.00
5 1999.80 1999.60 1999.40 1999.20 1999.00 1998.80 1998.60 1998.40 1998.20 1998.00
7 1428.43 1428.29 1428.14 1428.00 1427.86 1427.71 1427.57 1427.43 1427.29 1427.14
11 909.00 908.91 908.82 908.73 908.64 908.55 908.45 908.36 908.27 908.18
13 769.15 769.08 **769 768.92 768.85 768.77 768.69 768.62 768.54 768.46
17 588.18 588.12 588.06 588.00 587.94 587.88 587.82 587.76 587.71 587.65
19 526.26 526.21 526.16 526.11 526.05 **526 525.95 525.89 525.84 525.79
23 434.74 434.70 434.65 434.61 434.57 434.52 434.48 434.43 434.39 434.35
29 344.79 344.76 344.72 344.69 344.66 344.62 344.59 344.55 344.52 344.48
31 322.55 322.52 322.48 322.45 322.42 322.39 322.35 322.32 322.29 322.26
37 270.24 270.22 270.19 270.16 270.14 270.11 270.08 270.05 270.03 270.00
41 243.88 243.85 243.83 243.80 243.78 243.76 243.73 243.71 243.68 243.66
43 232.53 232.51 232.49 232.47 232.44 232.42 232.40 232.37 232.35 232.33
47 212.74 212.72 212.70 212.68 212.66 212.64 212.62 212.60 212.57 212.55
53 188.66 188.64 188.62 188.60 188.58 188.57 188.55 188.53 188.51 188.49
59 169.47 169.46 169.44 169.42 169.41 169.39 169.37 169.36 169.34 169.32
61 163.92 163.90 163.89 163.87 163.85 163.84 163.82 163.80 163.79 163.77
67 149.24 149.22 149.21 149.19 149.18 149.16 149.15 149.13 149.12 149.10
71 140.83 140.82 140.80 140.79 140.77 140.76 140.75 140.73 140.72 140.70
73 136.97 136.96 136.95 136.93 136.92 136.90 136.89 136.88 136.86 136.85
79 126.57 126.56 126.54 126.53 126.52 126.51 126.49 126.48 126.47 126.46
83 120.47 120.46 120.45 120.43 120.42 120.41 120.40 120.39 120.37 120.36
89 112.35 112.34 112.33 112.31 112.30 112.29 112.28 112.27 112.26 112.25
97 103.08 103.07 103.06 103.05 103.04 103.03 103.02 103.01 103.00 102.99
I used Excel, it took just a few minutes.
==============
Re other tutor's comments: 9997 is greater than 9409.
And, 9994 > 9409
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In Math (in the Number Theory especially), when people talk about the number of divisors of the given number, 1 (unit ONE) is ALWAYS
considered as a divisor, and is counted ONE time.
See, for example, this link
http://primes.utm.edu/glossary/xpage/tau.html
http://primes.utm.edu/glossary/xpage/tau.html
The solution of the problem was done by me under this link
https://www.algebra.com/algebra/homework/Rate-of-work-word-problems/Rate-of-work-word-problems.faq.question.1064533.html
https://www.algebra.com/algebra/homework/Rate-of-work-word-problems/Rate-of-work-word-problems.faq.question.1064533.html
For your convenience I copy and past it here again:
--------------------------
If the number has exactly 3 factors, it means that the number is the square of a prime number: N =  .
Then it has the factors 1 (one), p and .
Then it has the factors 1 (one), p and  .
Indeed, if the number is a prime number, it has only TWO factors: 1 (one) and itself.
If the number is not prime and is not the square of a prime, then it has more than 3 factors.
Therefore, to answer the problem's question, we must take the square of the largest two-digit prime number, which is .
Indeed, if the number is a prime number, it has only TWO factors: 1 (one) and itself.
If the number is not prime and is not the square of a prime, then it has more than 3 factors.
Therefore, to answer the problem's question, we must take the square of the largest two-digit prime number, which is 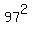 = 9409.
Answer. The number under the question is 9409. = 9409.
Answer. The number under the question is 9409.
Solved.
--------------------------
When Alan tries to argue with me, he simply demonstrates that he is not familiar with the subject.
-----------------------
Next is my notice to the person who posted it for the second time.
As I just said it was posted before, and solved and answered.
Now this request was repeated.
I am very sad that you can not recognize the correct solution which was developed and explained to you.
-----------------------
If you ARE NOT that person who posted it for the first time,
then simply IGNORE this notice. It is not to you . . .
|
|
|