.
x^2/y +y^2/x =9 ........eq1
1/x +1/y= 3/4............eq2
solve the simultaneous equations
~~~~~~~~~~~~~~~~~~~~~~~~~~~
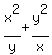 = 9 (1)
= 9 (1)
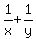 =
=  . (2)
In (1), multiply both sides by x*y. In 2), do the same. You will get an equivalent system (equivalent under the condition xy =/= 0):
. (2)
In (1), multiply both sides by x*y. In 2), do the same. You will get an equivalent system (equivalent under the condition xy =/= 0):
 = 9xy, (3)
x + y =
= 9xy, (3)
x + y =  . (4)
Now,
. (4)
Now,  =
= 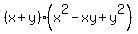 =
=  =
= 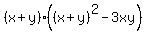 .
Next, replace here all instances of (x+y) by
.
Next, replace here all instances of (x+y) by  , according to (4), and you will get (3) in the form
, according to (4), and you will get (3) in the form
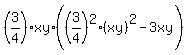 = 9xy.
Cancel 3xy in both sides. You will get
= 9xy.
Cancel 3xy in both sides. You will get
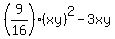 = 12.
Multiply both sides by 16. You will get
= 12.
Multiply both sides by 16. You will get
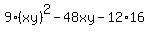 = 0,
= 0,
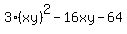 = 0. (5)
Introduce new variable u = xy. Then (5) becomes
= 0. (5)
Introduce new variable u = xy. Then (5) becomes
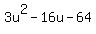 = 0.
Solve this quadratic equation using the quadratic formula. The roots are
= 0.
Solve this quadratic equation using the quadratic formula. The roots are
 = 8 and/or
= 8 and/or  =
= 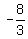 .
Thus the system (3),(4) is reduced to two independent and much simpler systems:
1) First system is
x + y = 6,
xy = 8
2) The second system is
x + y = -2,
xy =
.
Thus the system (3),(4) is reduced to two independent and much simpler systems:
1) First system is
x + y = 6,
xy = 8
2) The second system is
x + y = -2,
xy = 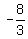 The major reduction is done.
The first system has two solutions (x,y) = (2,4) and (x,y) = (4,2).
The second system has two solutions (x,y) = (
The major reduction is done.
The first system has two solutions (x,y) = (2,4) and (x,y) = (4,2).
The second system has two solutions (x,y) = (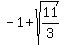 ,
,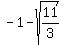 ) and (x,y) = (
) and (x,y) = (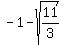 ,
,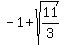 ).
).
Carefully check my math.