SOLUTION: A set of 7 positive integers has a median 3 and unique mode 4. If you add two 2's to the set the median and unique mode are then both equal 2. What is the mean of the new set

Let these be

A ≤ B ≤ C ≤ D ≤ E ≤ F ≤ G

So the middle number must be 3 

A ≤ B ≤ C ≤ 3 ≤ E ≤ F ≤ G

So there must be at least 2 4's among E,F and G.

There are only 3 integers for A, B and C, which are
1, 2, and 3, so there must be at least 2 1's, 2 2's or 2 3's.
Since there must be more 4's than anything else, there must
be more than two 4's, so there must be three 4's. So E, F 
and G must all be 4's.

A ≤ B ≤ C ≤ 3 ≤ 4 ≤ 4 ≤ 4

So there are only 5 possibilities:

1 ≤ 1 ≤ 2 ≤ 3 ≤ 4 ≤ 4 ≤ 4
1 ≤ 1 ≤ 3 ≤ 3 ≤ 4 ≤ 4 ≤ 4
1 ≤ 2 ≤ 2 ≤ 3 ≤ 4 ≤ 4 ≤ 4
1 ≤ 2 ≤ 3 ≤ 3 ≤ 4 ≤ 4 ≤ 4
2 ≤ 2 ≤ 3 ≤ 3 ≤ 4 ≤ 4 ≤ 4

Since we must add two 2's, there must
already be two 2's for if there were
only one 2, there wouldn't be enough
2's to be more than the three 4's. 
Only two of those have two 2's, so
we've narrowed it down to these two:

1 ≤ 2 ≤ 2 ≤ 3 ≤ 4 ≤ 4 ≤ 4
2 ≤ 2 ≤ 3 ≤ 3 ≤ 4 ≤ 4 ≤ 4 

Let's add two 2's to each of those:

1 ≤ 2 ≤ 2 ≤ 2 ≤ 2 ≤ 3 ≤ 4 ≤ 4 ≤ 4
2 ≤ 2 ≤ 2 ≤ 2 ≤ 3 ≤ 3 ≤ 4 ≤ 4 ≤ 4

Now we can eliminate the second one because 
the median is not 2.  So the only possibility is

1 ≤ 2 ≤ 2 ≤ 2 ≤ 2 ≤ 3 ≤ 4 ≤ 4 ≤ 4

So the mean is:



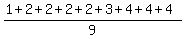
Answer: 

Edwin