.
If  and
and  with
with  it follows that
it follows that 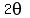 = ....
= .... 
the answer is  but I got only
but I got only  What did I do wrong?
What did I do wrong?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
You correctly determined that 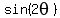 =
=  .
Notice that both
.
Notice that both  and
and  are positive, as it is (implicitly) stated by the condition.
Hence,
are positive, as it is (implicitly) stated by the condition.
Hence,  lies in QI.
Therefore
lies in QI.
Therefore  can be one of the two angles:
can be one of the two angles:  or
or  and CAN NOT be anything different.
Moreover, since
and CAN NOT be anything different.
Moreover, since  <
<  , the angle
, the angle  is less than
is less than  .
Therefore,
.
Therefore, 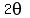 =
=  and CAN NOT be anything different.
and CAN NOT be anything different.