Question 106441This question is from textbook
: Are the following lines parallel, perpendicular or neither?
L1 through (9,2) and (3,-8)
L2 through (-3,5) and (5,-1)
m1= -8-2 = -6 = -1
3-(-9) 12 2
m2 = -1-5 = 4 = 1
5-(-3) 8 2
The lines are perpendicular
This question is from textbook
Answer by solver91311(24713)   (Show Source):
You can put this solution on YOUR website! You were certainly on the right track by computing the slopes of the two lines because we know that parallel lines have equal slopes, i.e.
 ,
and perpendicular lines have slopes that are the negative reciprocal of each other, i.e.
And I think you have the right idea about the formula for computing the slope given two points of a line. I think you just got lost in the arithmetic, especially with regard to addition of signed numbers.
So for the first line,  therefore  ; 
For the second line,  therefore  ; 
Since 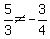 the lines are not parallel.
Since 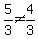 the lines are not perpendicular either.
The correct answer is "Neither"
By the way, if you carefully graph these two lines, at first glance they look as if they might be perpendicular, but if you compare the angles formed by the intersection of the lines to a known right angle, you will see that they are clearly not perpendicular after all.
One more "by the way"
I think you may have been using:
to compute the slope instead of the formula I used. In fact, it doesn't make any difference which of the points you call number 1 and which you call number 2 so long as you are consistent when you apply the formula.
The reason it doesn't make any difference is that  so  and therefore 
|
|
|
