SOLUTION: I have a 6 inch diameter ball. How many balls will fill a room 10ftx12ft with a 8ft ceiling (10x12x8=960)? This room has no furniture or obtrusion's to consider. I can visualize

Algebra ->  Bodies-in-space -> SOLUTION: I have a 6 inch diameter ball. How many balls will fill a room 10ftx12ft with a 8ft ceiling (10x12x8=960)? This room has no furniture or obtrusion's to consider. I can visualize       Log On


   

Question 1064392: I have a 6 inch diameter ball. How many balls will fill a room 10ftx12ft with a 8ft ceiling (10x12x8=960)? This room has no furniture or obtrusion's to consider.
I can visualize 8 balls occupying a 1ftx1ftx1ft space if the balls are set in straight rows from one another. 8 balls/cubic foot of space.
8 balls x 960 = 7,680 balls
BUT if I move the second level of balls over so they nestle into the depressed areas found between the first row of balls I am overwhelmed trying to figure that out.
I have looked online and see there is rounded questimate of .74, but I am not sure if this is what I need?
Do I simply take 8 balls/cubic ft x 960 cubic ft divide by .74 = ?
= 10,378 balls
Thanks

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
When packing spheres into a container,
there is always "wasted" empty space between the spheres.
There is also empty space between the spheres and the boundaries (floor, walls, ceiling) of the container.
The volume of a sphere with 6 inch diameter (3 inch radius) is
Volume%5Bball%5D=%284%2F3%29%2Api%2A%283in%29%5E3=36piin%5E3=about113.1in%5E3 .
A cube with 1 foot edges has a volume of
%2812in%29%5E3=1728in%5E3 .
With the packing you visualized first,
the fraction of the space filled with balls is
8%2A36%2Api%2F1728=about0.5236=52.36%2F100=%2252.36%25%22 .
You would fit only 8%2A960=7680 balls.

The alternate packing you propose is a better option,
especially for filling a large room with relatively small balls.
The height used up for one layer of balls is sqrt%283%29R=about1.732R rather than 2R .
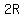For a 1 cubic foot container, even with that strategy,
you cannot achieve a very efficient packing of balls
with a diameter of 6in=0.5ft .

For the most efficient packing, the maximum theoretical fill ratio is,
as you found, 0.74=74%25 .
You can approach that ratio, if the size of your container
is large compared to the volume of 1 sphere.
The size of your container is
%2810ft%29%2A%2812ft%29%2A%288ft%29=960ft%5E3=960ft%5E3%2A%281728in%5E3%2Fft%5E3%29=1658880in%5E3 .
If you could fill 74% of that space with balls, you would fill
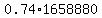0.74%2A1658880in%5E3=1227571.2in%5E3 .
The number of balls that fit in that "fillable" space is
1227571.2%2F113.1=10854.145 (rounded).
So, highlight%2810854%29 may be a good estimate.

For a more accurate calculation,
accounting for additional space wasted along floor, ceiling and walls,
we can calculates how many layers of balls fit into 8ft=96inches ,
at 0.1732%2A3in=5.196in per layer.
That would be 96%2F5.196=18.476 layers.
That is 18 layers, with some wasted space above the top layer.
Layers 1, 3, 5, etc would have %2820+balls%29%2A%2824balls%29=480balls .
Layers 2,,4,6,etc would have %2819balls%29%2A%2823balls%29=437balls .
with 18 layers, you would have
9%2A%28480balls%29%2B9%2A%28437balls%29=highlight%288235balls%29 .
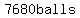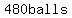That is better than 7680balls in 16 layers of 480balls per layer,
but it is far less than the 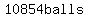10854balls estimate