.
X²-3x+1=0 find the value x5+1/x5
~~~~~~~~~~~~~~~~~~
In more understandable language, the formulation is as follows:
If "x" is the root of the equation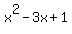 
= 0, find 
+ 
.
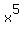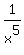You may try to solve this quadratic equation "analytically" (or numerically) and then calculate the value + .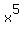
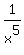But it is NOT the way to solve the problems like this. And they definitely expect ANOTHER solution from you.
There is elegant and canonical solution, and below I will show you how it works.
Let 
and 
be the two roots of the given quadratic equatio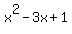n = 0.
Then = =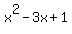 
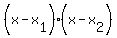, and therefore
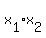= 1 and 
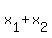= 3. (1)
In particular, it means that the roots of the given equation are reciprocal: = 
, = 
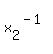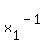. (2)
Moreover, if "x" is the root of the equation, then 
is another root. (3)
It is the same fact, simply expressed in other words.
And the statements (2) and (3) are consequences of the fact that the constant term of the given equation is equal to 1 (one).
So, we learned this:
if "x" is the root of the given equation, then is the root also, and, therefore,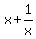 
= 3 due to (1) and (2).
Then, 
= 27 = 
+ 
+ 
+ 
= + 
+ 
+ = + 
+ = 
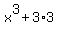+ = + + 9,
and therefore, + = 27 - 9 = 18. (Did you noticed that on the way I replaced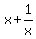 
by 3 due to (1) and (2) ? )
Similarly,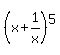 
= 
= 243 = +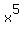 
+ 
+ 
+ 
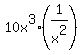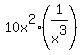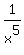+ ( I used binomial expansion for 
)
= + + 
+ 
+ 
= + + 
+ 
= + + 
+ 
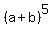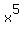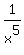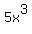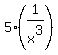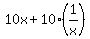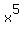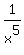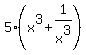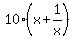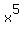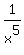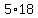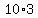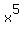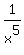= + + 120,
and therefore, 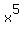+ 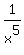= 243 - 120 = 123.
Answer. If x is the root of the equation 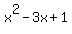= 0, then 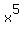+ 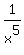= 123.
Solved.
(