Question 1063998: 3 years ago a man is four times the age of the daughter. If the product of their ages is 430 what are their present ages?
Found 3 solutions by addingup, ikleyn, MathTherapy:
Answer by addingup(3677)   (Show Source): (Show Source):
You can put this solution on YOUR website! m-3 = 4(d-3)
m = 4(d-3)+3
m = 4d-12+3
m = 4d-9
and
m*d = 430 here substitute for m:
(4d-9)*d = 430
d^2*4-9d-430 = 0
Now this equation is in standard quadratic form ax^2+bx+c = 0, so let's work it, the quadratic formula is (-b+/- sqrt(b^2-4ac))/2a:
d = [-(-9)+sqrt((-9)^2-4)*4(-430)]/2*4
d = [-(-9)+sqrt(81+(-16)*(-430))]/2*4
d = [-(-9)+sqrt(81+6880)]/2*4
d = [-(-9)+sqrt6961]/2*4
d = (9+sqrt6961)/8 Now you would repeat the exercise to solve when b is negative.
But We're not looking for a negative number, so let's solve what we've got:
d = 11.55
---------------------------
Check:
father - 3 = 4(d-3)
f-3 = 4(11.55-3)
f-3 = 34.2
f = 37.2
the problem says f*d = 430
37.2*11.55 = 429.66 round it off, it's 430 Correct
:
John
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Age word problems with non-integer solutions ARE DEFECTIVE by the definition.
~~~~~~~~~~~~~~~~~~~~~~
Specially for the "Math-Therapy" tutor (after his solution) and to the author of the problem:
I still think that this problem (as it was written and came in the post) IS/was DEFECTIVE by its wording/logic/meaning construction.
God save me of such problems !!
------------------------------
My advise to "Math-Therapy" is to delete/erase his rebukes to tutors and redirect them to the person who wrote/posted the formulation.
In math problem formulations EACH WORD COUNTS !!!
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! 3 years ago a man is four times the age of the daughter. If the product of their ages is 430 what are their present ages?
The original problem for this was:
https://www.algebra.com/algebra/homework/word/age/Age_Word_Problems.faq.question.776905.html
https://www.algebra.com/algebra/homework/word/age/Age_Word_Problems.faq.question.776905.html
The difference with the above problem (# 1063998) is that it failed to include the words: "IS NOW."
As such, I agree with IKLEYN that it is DEFECTIVE, as age problems with ages that are NON-INTEGERS, are nonsense, in my opinion.
I think IKLEYN misunderstood me. When I referred to the 3 people who responded, I was talking about the 3 who responded to the ORIGINAL problem (# 776905),
not the CURRENT problem (# 1063998). I IMPLORE you to LOOK at the ORIGINAL problem (# 776905) and you'll see what I'm talking about.
This is UNBELIEVABLE! 3 other persons responded to the OLDER math problem (# 776905) and all 3 were UNABLE to solve this simple problem. Why so???
And, these people call themselves, TUTORS!
This is the ORIGINAL problem, solved a LONG time ago and ONLY yours truly's answer was correct.
3 years ago a father was 4 times as old as his daughter is now. The product of their ages is 430. Calculate their present ages.
Let daughter's, and father's current ages be D, and F, respectively
Then: F - 3 = 4D ----- F = 4D + 3 ----- eq (i)
Also FD = 430 ------ eq (ii)
D(4D + 3) = 430 ----- Substituting 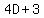 for F in eq (ii) for F in eq (ii)

Solve this to get daughter's age. Then find father's: 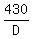
You should get:
Daughter's current age: 
Father's current age: 
|
|
|