|
Question 106386: Please help me. I really had a hard time figuring out how to get the number of fractions using a formula/equation for this problem. However, I noticed a pattern for this. Numerator that is divisible by 3 is not part of the fraction. My problem is, how can I know the number of fractions with numerator (from numbers 1 to 166) not divisible by 3. Can somebody give me a hand how to solve this one. Thanks in advance.
Fractions of the form a/b are created such that a and b are positive integers and a+b=333. How much such fractions are less than one and cannot be reduced? (That is, the numerator and denominator have no common factor).
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm a little unsure if this is the complete answer to your problem, but perhaps it will give you a start.
First off, you know that 0 < a < b, since the fraction is < 1, and 0/333 reduces to 0.
Second, we know that 0 < a < 167, and 166 < b < 333.
Third, we know that a = 333 - b.
Our fraction can be represented as 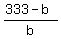 , or put another way, , or put another way, 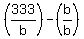
Now the prime factorization of 333 is 3 X 3 X 37.
This tells me that any  where where  has 3 or 37 as a factor would be reduceable. has 3 or 37 as a factor would be reduceable.
There are 55 numbers in the range 0 < a < 167 that have 3 as a factor, and 4 numbers in that range that have 37 as a factor. However, these two sets have one number in common, namely 111. Hence the number of numerators that result in a reduceable fraction is 55 plus 4 minus 1, or 58. Since there are 166 possible fractions excluding the non-reduceable condition, the number of non-reduceable fractions would be 108.
I think.
|
|
|
| |