Question 1063548: At a church a total of $500.00 was collected. There were men, women, and kids. Each man put in five dollars each woman one dollar and each kid one cent. If there was a total of 500 people, how many were men? How many were women? how many were kids?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52794)   (Show Source):
You can put this solution on YOUR website! .
At a church a total of $500.00 was collected. There were men, women, and kids. Each man put in five dollars each woman one dollar
and each kid one cent. If there was a total of 500 people, how many were men? How many were women? how many were kids?
~~~~~~~~~~~~~~~~~~~~~~~
It is clear that the number of kids is a multiple of 100.
If the number of kids is exactly 100, then the sum of men and women is 400,
which is impossible to collect the odd number of dollars (500 - 1 = 499).
Similarly, the number of kids can not be 300, by the same reason.
If the number of kids is 200, then you have an equation for the number of men "m"
5m + (300-m) = 498 ---> 4m = 498-300 ---> m = 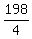 = not an integer,
so it is not possible.
If the number of kids is 400, then you have an equation
5m + (100-m) = 496 ---> 4m = 496-100 ---> m = 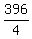 = 99.
Also, it is clear that 500 kids is not the option.
So, we just get the unique answer: 99 men, 1 women and 400 kids.
Answer. 99 men, 1 women and 400 kids.
Answer by Edwin McCravy(20056)  (Show Source):
|
|
|
