.
Solve the following equations for 0deg <= x <= 360deg:
(i) cos 2x cos x = sin 4x sin x
(ii) cos x + cos 2x + cos 3x + cos 4x = 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
I will solve (ii).
cos(x) + cos(2x) + cos(3x) + cos(4x) = 0. (1)
Use the general formula of Trigonometry
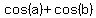 =
= 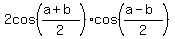 . (2)
You have
cos(x) + cos(4x) =
. (2)
You have
cos(x) + cos(4x) = 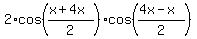 =
= 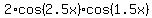 ,
cos(2x) + cos(3x) =
,
cos(2x) + cos(3x) = 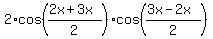 =
= 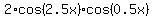 .
Therefore, the left side of the original equation is
cos(x) + cos(2x) + cos(3x) + cos(4x) = 2*cos(2.5x)*cos(1.5x) + 2*cos(2.5x)*cos(0.5x) = 2*cos(2.5x)*(cos(1.5x) + cos(0.5x)).
Hence, the original equation is equivalent to
2*cos(2.5x)*(cos(1.5x) + cos(0.5x)) = 0, or, canceling the factor 2*cos(2.5x),
cos(1.5x) + cos(0.5x) = 0. (3)
Again, apply the formula (2) to the left side of (3). You will get an equivalent equation
.
Therefore, the left side of the original equation is
cos(x) + cos(2x) + cos(3x) + cos(4x) = 2*cos(2.5x)*cos(1.5x) + 2*cos(2.5x)*cos(0.5x) = 2*cos(2.5x)*(cos(1.5x) + cos(0.5x)).
Hence, the original equation is equivalent to
2*cos(2.5x)*(cos(1.5x) + cos(0.5x)) = 0, or, canceling the factor 2*cos(2.5x),
cos(1.5x) + cos(0.5x) = 0. (3)
Again, apply the formula (2) to the left side of (3). You will get an equivalent equation
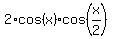 = 0. (4)
Equation (4) deploys in two independent separate equations:
1. cos(x) = 0 ---> x =
= 0. (4)
Equation (4) deploys in two independent separate equations:
1. cos(x) = 0 ---> x =  , k = 0, +/-1, +/-2, . . .
2. cos(x/2) = 0 ---> x =
, k = 0, +/-1, +/-2, . . .
2. cos(x/2) = 0 ---> x =  , k = 0, +/-1, +/-2, . . .
So, in the given interval the original equation has the roots 0,
, k = 0, +/-1, +/-2, . . .
So, in the given interval the original equation has the roots 0,  ,
,  ,
,  or 0°, 90°, 180°, 270°.
But these are not ALL the roots.
There is one more family of roots.
Do you remember I canceled the factor 2*cos(2.5x) ?
Of course, I must consider (and add !) all the solutions of the equation
cos(2.5x) = 0.
They are 2.5x =
or 0°, 90°, 180°, 270°.
But these are not ALL the roots.
There is one more family of roots.
Do you remember I canceled the factor 2*cos(2.5x) ?
Of course, I must consider (and add !) all the solutions of the equation
cos(2.5x) = 0.
They are 2.5x =  , k = 0, +/-1, +/-2, . . .
or, which is the same,
, k = 0, +/-1, +/-2, . . .
or, which is the same,
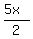 =
=  +
+  , k = 0, +/-1, +/-2, . . .
So, these additional solutions are x =
, k = 0, +/-1, +/-2, . . .
So, these additional solutions are x = 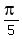 ,
, 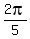 ,
, 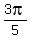 ,
, 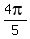 PLUS
PLUS  , k = 0, +/-1, +/-2, . . .
The final answer is: There are two families of solutions.
One family is 0°, 90°, 180° and 270°.
The other family is 36°, 72°, 108°, 144°, 180°, 216°, 252°, 288°, 324°.
, k = 0, +/-1, +/-2, . . .
The final answer is: There are two families of solutions.
One family is 0°, 90°, 180° and 270°.
The other family is 36°, 72°, 108°, 144°, 180°, 216°, 252°, 288°, 324°.
Solved.