Question 1063200: I need to solve this equation for 0 < x< 2pi
-2tan(-2x + 4pi/3) = 2sqrt3
Found 2 solutions by stanbon, ikleyn:
Answer by stanbon(75887)   (Show Source): (Show Source):
You can put this solution on YOUR website! I need to solve this equation for 0 < x< 2pi
-2tan(-2x + 4pi/3) = 2sqrt3
-----
tan(-2x+(4/3)pi) = -sqrt(3)
----
Take the arctan of both sides to get:
-2x+(4/3)pi = (2/3)pi or (5/3)pi
-----
-2x = (-2/3)pi or (1/3)pi
------
x = (1/3)pi or (-2/3)pi
------------------------
Cheers,
Stan H.
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I need to solve this equation for 0 < x < 2pi
-2tan(-2x + 4pi/3) = 2sqrt3
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 = =  -----> (divide both sides by (-2) ) ---> -----> (divide both sides by (-2) ) --->
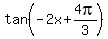 = =  ---->
The last equation has solutions ---->
The last equation has solutions  = = 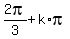 , k = 0, +/-1, +/-2, , , , .
Let's derive an expression for x from this: , k = 0, +/-1, +/-2, , , , .
Let's derive an expression for x from this:
 = = 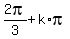 ----> ---->  = = 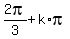 ----> ----> 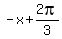 = = 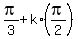 ----> x = ----> x = 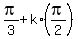 , k = 0, +/-1, +/-2, , , , .
In the given interval ( , k = 0, +/-1, +/-2, , , , .
In the given interval ( , , )
x = )
x =  , , 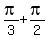 , , 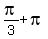 , , 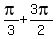 are the solutions.
Answer. In the given interval the solutions are = are the solutions.
Answer. In the given interval the solutions are =  , , 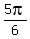 , ,  , ,  . (See the plot below) . (See the plot below)

Plots y = 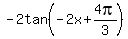 and y = and y = 
To see more examples of solved trigonometry equations with detailed solutions, look into the lessons
- Solving simple problems on trigonometric equations
- Solving typical problems on trigonometric equations
- Solving more complicated problems on trigonometric equations
- Solving advanced problems on trigonometric equations
- Proving Trigonometry identities
- OVERVIEW of lessons on calculating trig functions and solving trig equations
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Trigonometry: Solved problems".
|
|
|