Question 1062886: A regular decagon is inscribed inside a circle. The perimeter of the decagon is 50 units.
A: What is the approximate measure of the radius (rounded to the nearest hundredth of a unit)?
B: What is the approximate area of the circle (rounded to the nearest whole square unit)?
Select only one answer each for parts A and B.
A: 8.09
A: 2.63
A: 7.69
A: 4.25
B: 22
B: 186
B: 206
B: 57
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! The perimeter of a 10 sided object is 50 units, so each side is 5 units.
This divides the polygon into 10 isosceles triangles, each of which has a radius for the two equal sides.
Half the length of a side is 2.5 units
The central angle is 36 degrees, and it is 18 degrees for the triangle whose sides are the radius, half the side length and the apothem.
sin 18=2.5/radius (the hypotenuse)
radius=2.5/sin 18=8.09 units. A
The area will be pi*(8.09)^2, and that will be greater than 3*64 (192), so it has to be 206 for B.
The actual answer is 205.61 rounding upward to 206.
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A regular decagon is inscribed inside a circle. The perimeter of the decagon is 50 units.
A: What is the approximate measure of the radius (rounded to the nearest hundredth of a unit)?
B: What is the approximate area of the circle (rounded to the nearest whole square unit)?
Select only one answer each for parts A and B.
A: 8.09
A: 2.63
A: 7.69
A: 4.25
B: 22
B: 186
B: 206
B: 57
~~~~~~~~~~~~~~~~~~~~
Let me show you how to estimate it without using calculator, computer, trigonometric tables and the Internet.
Using your (or my) BRAIN only !!!
Since the perimeter is 50 units, the one side length is 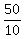 = 5 units.
The central angle leaning one side is = 5 units.
The central angle leaning one side is 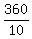 = 36 degrees.
One half of this angle is 18 degrees: = 36 degrees.
One half of this angle is 18 degrees:  = 18 degrees ~ = 18 degrees ~  of the radian (approximately).
Hence, of the radian (approximately).
Hence,  =~ =~  , approximately.
Then the apothem, which is the height of the single central triangle, is about , approximately.
Then the apothem, which is the height of the single central triangle, is about 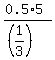 = 2.5*3 = 7.5, approximately.
Then the area of one single central triangle is about = 2.5*3 = 7.5, approximately.
Then the area of one single central triangle is about 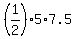 = 18.75.
Take it 10 times, and you will get the number 187.5 for the area.
Which number from the list is close to it? = 18.75.
Take it 10 times, and you will get the number 187.5 for the area.
Which number from the list is close to it?
It is very useful if somebody will show you how to do it.
At least once in your life !!
-----------------------------------
OK, it looks like I made some mistake, comparing with the more accurate answer of the other tutor.
Nevertheless, my error of 10% is allowable for such a crude estimation.
|
|
|