Question 1062846: Obtain the equation of a straight line that is symmetric to line l: y=x-3 with respect to line m: (-1/3)x-(1/3).
Answer by Fombitz(32388)   (Show Source):
You can put this solution on YOUR website! First find the point of intersection,
So then,
Now find the perpendicular bisector of the line,  },
you know that the slope of the bisector is equal to  since perpendicular lines have slopes that are negative reciprocals.
So the line has the form 
Choose a point on the line.
I'll choose (5,-2).
So the equation of the perpendicular bisector using point slope form would be,
The intersection point of the perpendicular bisector with the original line can be found,
and
(7,4)
So then using (5,-2) as the center point and (7,4) as the intersection point, find the corresponding intersection point with the symmetric line.
To go from the center point to the intersection point, you move 2 units in x and 6 units in y. The intersection point of the symmetric line will have the same value but just different sign.
So starting at (5,-2) you would move -2 in the x and -6 in the y.
(5,-2)+(-2,-6)=((3,-8)
So now you know the symmetric line goes through (3,-8) and (2,-1).
Find the slope,
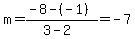
Then use the point slope form,
.
.
.
|
|
|
