Question 1062832: Find the arithmetic and geometric mean of the series 1,2,4,8,16,....,2^n find also harmonic mean
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the arithmetic and geometric mean of the series 1,2,4,8,16,....,2^n find also harmonic mean
~~~~~~~~~~~~~~~~~~~~~
1. To find the ARITHMETIC MEAN, find the sum of the first (n+1) terms of the geometric progression, and then divide the sum
by the number of terms (n+1). You should divide by (n+1) (and not by "n", because there are (n+1) terms in the sequence from 1 to  .
It is SO CLEAR that I will do not do it for (and instead of) you.
It will be MUCH BETTER if you do it on your own. .
It is SO CLEAR that I will do not do it for (and instead of) you.
It will be MUCH BETTER if you do it on your own.
2. To find the GEOMETRIC MEAN, find the product of the first "n" terms of the progression, and then take the (n+1)-th root of the product.
We take the (n+1)-th root of the product (and not the n-th degree) because there are n+1 multipliers (factors) in the product
from 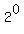 to to  .
The product of the first "n" terms is
P = .
The product of the first "n" terms is
P = 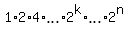 = 2 in degree = 2 in degree 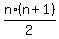 .
This index .
This index  (I mean the upper index, which is "the degree") arises because
the indexes of "2" are 0, 1 , 2, 3, . . . k, . . . n, and their sum is
0 + 1 + 2 + 3 + . . . + n = (I mean the upper index, which is "the degree") arises because
the indexes of "2" are 0, 1 , 2, 3, . . . k, . . . n, and their sum is
0 + 1 + 2 + 3 + . . . + n =  = the sum of the first "n" natural numbers.
Again, P = 2 in degree = the sum of the first "n" natural numbers.
Again, P = 2 in degree 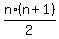 .
Then the (n+1)-th degree root of P is 2^(n/2), or, which is the same, .
Then the (n+1)-th degree root of P is 2^(n/2), or, which is the same,  .
Thus the geometric mean is 2^(n/2) = .
Thus the geometric mean is 2^(n/2) =  . .
3. The HARMONIC MEAN is
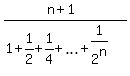 (H)
where the denominator is the sum of inverse values to the original sequence.
The numerator is (n+1) because there are n+1 term in our original sequence 1, 2, 4, . . . (H)
where the denominator is the sum of inverse values to the original sequence.
The numerator is (n+1) because there are n+1 term in our original sequence 1, 2, 4, . . .  .
See the definition of the "harmonic mean" in this Wikipedia article.
The denominator of the formula (H) above is the sum of the geometric sequence, again.
So, it is very similar to what you just saw in the n.1 (#1) above.
Follow to instructions of the #1. .
See the definition of the "harmonic mean" in this Wikipedia article.
The denominator of the formula (H) above is the sum of the geometric sequence, again.
So, it is very similar to what you just saw in the n.1 (#1) above.
Follow to instructions of the #1.
Solved.
There is a bunch of lessons on arithmetic progressions in this site:
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Mathematical induction and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
There is a bunch of lessons on geometric progressions, too:
- Geometric progressions
- The proofs of the formulas for geometric progressions
- Problems on geometric progressions
- Word problems on geometric progressions
- One characteristic property of geometric progressions
- Solved problems on geometric progressions
- Fresh, sweet and crispy problem on arithmetic and geometric progressions
- Mathematical induction and geometric progressions
- Mathematical induction for sequences other than arithmetic or geometric
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topics
"Arithmetic progressions" and "Geometric progressions".
|
|
|