4 mothers with four children walk in for a interview. Find the no of ways
to schedule this interview such that no child is interviewed before
her mother.
Suppose that:
mother A1 has daughter A2, and
mother B1 has daughter B2, and
mother C1 has daughter C2, and
mother D1 has daughter D2.
Then I claim the answer is the same as the number of
distinguishable permutations of AABBCCDD, which is
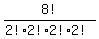
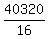
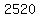Why?
Suppose the interviewing office is on the left and the
8 people are standing in line right to left waiting to
be interviewed.
For illustrative purposes, take the arbitrary selected
permutation DACDBBAC, written with a space after each,
with the office on the left:
Office, D ,A ,C ,D ,B ,B ,A ,C
We can always fill the spaces with the subscripts 1 and 2,
so that each letter with a 1 subscript is left of that same
letter with a 2 subscript. That is, there is only 1 way to
insert the subscripts in those spaces so that each mother
stands in the line left of her daughter and therefore
interviews before her daughter. That one way in this
permutation is:
Office, D1 ,A1 ,C1 ,D2 ,B1 ,B2 ,A2 ,C2.
So the answer is the number of distinguishable permutations of
AABBCCDD, which again is:
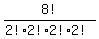
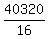
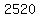Edwin
