SOLUTION: A bank contains 8 more pennies than nickels and 3 more dimes than nickels. If the total amount of money in the bank is $3.10, find the number of dimes in the bank.

Algebra ->  Expressions-with-variables -> SOLUTION: A bank contains 8 more pennies than nickels and 3 more dimes than nickels. If the total amount of money in the bank is $3.10, find the number of dimes in the bank.      Log On


   

Question 1062665: A bank contains 8 more pennies than nickels and 3 more dimes than nickels. If the total amount of money in the bank is $3.10, find the number of dimes in the bank.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617) About Me  (Show Source):
You can put this solution on YOUR website!
system%28p-n=8%2Cd-n=3%2C0.01p%2B0.05n%2B0.1d=3.1%29

system%28p=8%2Bn%2Cd=3%2Bn%2Cp%2B5n%2B10d=310%29

First two equations are in terms of n. Substitute for them in the money-count equation and solve first for n.

Answer by ikleyn(52787) About Me  (Show Source):
You can put this solution on YOUR website!
.
A bank contains 8 more pennies than nickels and 3 more dimes than nickels. If the total amount of money in the bank is $3.10,
find the number of dimes in the bank.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

This problem is for ONE unknown. Not for 3 !! 

Let "n" be the number of nickels.

Then the number of pennies is (n+8) and the number of dimes is (n+3).

Each penny contributes 1 cent to the total. In all, (n+8) pennies contribute (n+8) cents to the total.

Each nickel contributes 5 cents to the total. "n" nickels contribute 5n cents to the total.

Each dime contributes 10 cents to the total. (n+3) dimes contribute 10(n+3) cents to the total.

Therefore, your "value" equation is 

(n+8) + 5n + 10(n+3) = 310 cents.

n + 8 + 5n + 10n + 30 = 310,

16n + 38 = 310  --->  16n = 310-38  --->  16n = 272  --->  n = 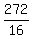272%2F16 = 17.

Thus the number of nickels is 17.

Then the number of pennies is (17+8) = 25  and  the number of dimes is (17+3) = 20.

Check. 25 + 17*5 + 10*20 = 

Answer.  The number of pennies is 25, the number of nickels is 17  and  the number of dimes is 20.

Solved.

The lesson to learn from the solution: This problem is for ONE unknown. Not for 3 !!

When you solve the problems like this one, your first step is to select a major unknown.
Then you express other unknowns via the major one.
Then you construct your equation.
Then you solve it.


For coin problems and their detailed solutions see the lessons in this site:
    - Coin problems
    - More Coin problems
    - Solving coin problems without using equations
    - Kevin and Randy Muise have a jar containing coins
    - Typical coin problems from the archive
    - Solving coin problems mentally by grouping without using equations
    - Santa Claus helps solving coin problem

Read them attentively and become an expert in this field.

Also, you have this free of charge online textbook in ALGEBRA-I in this site
    - ALGEBRA-I - YOUR ONLINE TEXTBOOK.

The referred lessons are the part of this online textbook under the topic "Coin problems". 


To make you laugh, I'll show you another approach which allows to solve the problem without using equations.


For the moment, take out 8 pennies and 3 dimes from the collection (mentally, of course).

Then you have equal number of pennies, nickels and dimes, and the collection is worth 310 - 8 - 30 = 272 cents.

Hence, you can group the remaining coins in sets (1 penny, 1 nickel, 1 dime) each.

Each such set is worth 1 + 5 + 10 = 16 cents.

How many such sets do you have ? - But of course, 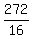272%2F16 = 17.

Hence you have 17 nickels in your collection.

And so on . . .

Solved (two times).