SOLUTION: In the square ABCD. AE is an angle bisector of BAC, and EF is perpendicular to AC. If AB = 4 cm, then the length of AE is ..... my answer is 3 root 2. But the answer key has differ

Algebra ->  Triangles -> SOLUTION: In the square ABCD. AE is an angle bisector of BAC, and EF is perpendicular to AC. If AB = 4 cm, then the length of AE is ..... my answer is 3 root 2. But the answer key has differ      Log On


   

Question 1062427: In the square ABCD. AE is an angle bisector of BAC, and EF is perpendicular to AC. If AB = 4 cm, then the length of AE is ..... my answer is 3 root 2. But the answer key has different result. Please help
Found 2 solutions by rothauserc, ikleyn:
Answer by rothauserc(4718) About Me  (Show Source):
You can put this solution on YOUR website!
AE^2 = AF^2 + EF^2
:
AF = (1/2) * length of diagonal = (1/2) * (4 * square root(2)) = 2 * square root(2)
:
tangent(22.5) = EF / (2 * square root(2))
:
EF = (0.414) * (2 * square root(2)) = 0.828 * square root(2)
:
Note that tangent(22.5) = 0.414
:
AE^2 = (2 * square root(2))^2 + (0.828 * square root (2))^2 = 9.37
:
*********
AE = 3.06 cm
*********
:

Answer by ikleyn(52915) About Me  (Show Source):
You can put this solution on YOUR website!
.
In the square ABCD. AE is an angle bisector of BAC, and EF is perpendicular to AC. If AB = 4 cm, then the length of AE is .....
my answer is 3 root 2. But the answer key has different result. Please help
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

There are two ways to solve it.

Solution 1 

AE is  the angle bisector of BAC.

It is (well ?) known fact that the angle bisector divides the opposite side proportionally to adjacent sides. 

    For the proof, see the lesson On what segments the angle bisector divides the side of a triangle in this site.

In your case it means that

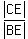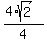abs%28CE%29%2Fabs%28BE%29 = abs%28AC%29%2Fabs%28AB%29 = %284%2Asqrt%282%29%29%2F4 = sqrt%282%29.

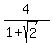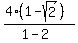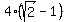Then  |BE| = 4%2F%281+%2B+sqrt%282%29%29 = (after rationalizing the denominator) = %284%2A%281-sqrt%282%29%29%29%2F%281-2%29 = 4%2A%28sqrt%282%29-1%29. 

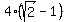Answer.  |BE| = 4%2A%28sqrt%282%29-1%29.

Solution 2 

The advanced people know (or can calculate) that tan(BAC) = tan(22.5°) = 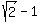sqrt%282%29-1.

See, for example, the lesson 

     - Trigonometric functions of half argument - Examples

     - Miscellaneous Trigonometry problems 

in this site.

Then |BE| = |AB|*tan(BAC) = 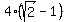4%2A%28sqrt%282%29-1%29.

The same answer as in the Solution 1.


What I do NOT understand in this problem is (are) the words and info related to EF.
It is not relevant to the major content of the problem.