Question 1062037: The answer given by one tutor doesn't match the one answer and the one reason behind the answer to this question, as indicated by the solutions at the back of my textbook, so I'm reposting. Can some other tutor please help??
Let A: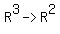 and B: and B: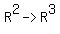 , so that BA: , so that BA: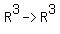 . Is BA an invertible map? . Is BA an invertible map?
Answer by rothauserc(4718)   (Show Source): (Show Source):
You can put this solution on YOUR website! A is a projection map, that is, (x, y, z) ----> (x, y)
:
B is an embedding map, that is, (x, y) -----> (x, y, 0)
:
AB is the identity map onto R^2, (x, y) ----A--> (x, y, z) ---B--> (x, y)
:
We can say that A is the left inverse of B which is equivalent to B is the right inverse of A
:
However, the composition BA does not give the identity map
:
For example,
:
(0, 0, 1) ----> (0, 0, 0) ----> (0, 0) for infinitely many z's
|
|
|