Find each exact value if 0 < x < pi/2 and 0 < y < pi/2
Cos(x-y) if sinx= 7/25 and cosy= 2/3
This is what I have so far:
cosa•cosB+sina•sinB
(7/25)(2/3)+(7/25)(sqrt5/3)
14/75+7sqrt5/75
14+7sqrt5/75
I'm not sure if I'm finished with the problem or if I have more steps or if I have just done the problem completely wrong. The answer doesn't match the key so I'm curious as to what I'm doing wrong. Thank you!
Find each exact value if 
cos (A - B) = cos A cos B + sin A sin B ---- Difference of 2 angles' formula
cos (x - y) = cos x cos y + sin x sin y ---- Replacing A with x, and B with y
It's obvious that we need cos x and sin y
We see that a 7-24-25 Pythag triple ensues, and therefore, x = 24
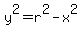
We now have: 
_____
We now have: 
cos (x - y) = cos x cos y + sin x sin y now becomes:
cos (x - y) =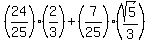 
------- Substituting 
Up to this point, you seem to have gotten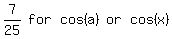 
, but 
.
You should be able to complete it, now that you know where your mistake was.
Note that since it was stated that: , the angles are in the 1st quadrant.
