Question 1061926: An accountant rides a bus part of the way to work every day and walks the rest of the way. The bus averages 35 mph, and the accountant walks at a speed of 6 mph. The distance from home to work is 18 mi, and the total time for the trip
2 hr. Find how far the accountant walks and how far he rides the bus.
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An accountant rides a bus part of the way to work every day and walks the rest of the way.
The bus averages 35 mph, and the accountant walks at a speed of 6 mph. The distance from home to work is 18 mi,
and the total time for the trip 2 hr. Find how far the accountant walks and how far he rides the bus.
~~~~~~~~~~~~~~~~~~~~~~~~~~
Let "x" be the distance "by bus", and let "y" be the distance "walking".
Then your equations are
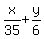 = 2, (1)
x + y = 18. (2)
In equation (1), = 2, (1)
x + y = 18. (2)
In equation (1),  is the time spent by the bus, and is the time spent by the bus, and 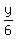 is the time walking.
To solve the system (1) and (2), first simplify it. For it, multiply (1) by 35*6 (the common denominator). You will get
6x + 35y = 420, (1') and
x + y = 18. (2')
Now express x = 18-y from (2') and then substitute it into (1') by replacing x. You will get
6*(18-y) + 35y = 420.
It is single equation for one unknown y. Simplify and solve it
108 - 6y + 35y = 420,
29y = 420 - 108 = 312 ---> y = is the time walking.
To solve the system (1) and (2), first simplify it. For it, multiply (1) by 35*6 (the common denominator). You will get
6x + 35y = 420, (1') and
x + y = 18. (2')
Now express x = 18-y from (2') and then substitute it into (1') by replacing x. You will get
6*(18-y) + 35y = 420.
It is single equation for one unknown y. Simplify and solve it
108 - 6y + 35y = 420,
29y = 420 - 108 = 312 ---> y = 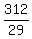 .
Thus you found that the distance walking is .
Thus you found that the distance walking is 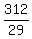 miles.
Then the "bus" way is miles.
Then the "bus" way is 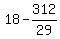 miles. miles.
You see these "curved" uneven numbers and, probably, think "why it is so?"
It is so because your numbers are such.
When I see such numbers, I think about the author.
May be, he specially invented these numbers to create the "true" "accountant problem".
May be, he never solved this problem on his own.
But in any case, I showed you how to solve it.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|