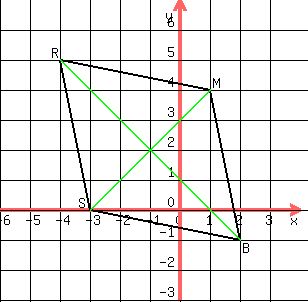
Question 1061873: The coordinates of the vertices of parallelogram RMBS are R(–4, 5), M(1, 4), B(2, –1), and S(–3, 0).Using the diagonals, prove that RMBS is a rhombus. Show all your work and state appropriate formulas and theorems used.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The problem with formulas and theorems (and with names and definitions) is that different people call them, see them, and write them differently.
Your teacher may live next door to me, and we still may use a "different language" for math,
so your teacher may see my solution as wrong (or copied from a foreign source).
You will need to use your judgement to translate what I write to the specific language your teacher prefers.
There may be also formats your teacher prefers, such as "two column proofs."
I assume that your teacher's definition of rhombus is
"a quadrilateral with four congruent sides," or
"a quadrilateral whose sides all have the same length."
With that definition a square is also a rhombus.
What I would do to prove that RMBS is a RhoMBuS is
1) prove that where the diagonals cross is the midpoint for both (they "bisect each other"), and
2) prove that the product of their slopes is  (they are perpendicular). (they are perpendicular).
That would involve formulas called the "midpoint formula" and the "slope" formula,
and a theorem that says that if the product of the slopes of two lines is  the lines are perpendicular. the lines are perpendicular.
The other theorem I would use can be stated as
"if a quadrilateral's diagonals perpendicularly bisect each other,
it is a rhombus."
With some luck, you have been taught that in some way.
Maybe in your class that was half of a theorem that said "if and only if," or "the converse is also true."
Maybe the theorem had a name, or a number.
Maybe the wording was a little different.
Maybe in your class that was two theorems:
one stating that if diagonals bisect each other it is a parallelogram,
and another stating that if the diagonals of a parallelogram are perpendicular, it is a rhombus.
MIDPOINTS:
For the segment connecting points 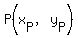 and and 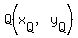 , ,
the coordinates of the midpoint are
 and and  . .
Maybe the points were not P and Q in the formula you were taught.
You can use whatever names you want for the points,
but if you use B in your formula it could get confusing.
For diagonal RB, the coordinates of the midpoint are
 --> --> --> --> . .
For diagonal MS, the coordinates of the midpoint are
 --> --> --> --> . .
So, the diagonals go through a common point that is the midpoint for both,
which means that either they are both on the same line (and they would have the same slope),
or they are segments that intersect at just one point that is a common midpoint, bisecting each other.
SLOPES:
For a segment PQ, connecting points 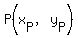 and and 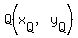 , ,
the slope is
 . .
For diagonal RB, the slope is
 --> --> --> --> --> --> . .
For diagonal MS, the slope is
 --> --> --> --> . .
The product of the slopes of RB and MS is
 , therefore , therefore
by the theorem that you can name whatever way it was named in your class,
RB and MS are perpendicular segments.
Since diagonals RB and MS are perpendicular segments that bisect each other,
by the theorem that you can name whatever way it was named in your class,
RMBS is a  . .
NOTE:
It is not a square, because the diagonals have different lengths.
Their pength can be calculated by the "distance formula,"
which for points 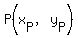 and and 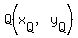 can be written as can be written as
 . .
Note that the expressions in brackets are the same as numerator and denominator in the slope formula,
so we have them already calculated.


|
|
|