Question 1061858: Hi
I am asking for a tutor to look and see if my answer is correct
A certain virus infects one in every 500 people. A test used to detect the virus in a person is positive 90% of the time if the person has the virus and 10% of the time if the person does not have the virus. Let A be the event "the person is infected" and B be the event "the person tests positive."
"What is the probability that a person does not have the virus given that they have tested negative." Of the 180 people who are infected, .1(180)= 18 will text negative. Of the 99800 people who are not infected, .9(99800)= 89820 will test negative. Of the 89820+ 18= 89838 people who tested negative 89820 do not have the virus so the probability a person who tested negative does not have the virus is 89820/89832= 0.999 or about 99.9%.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I suspect that the answer may end up being almost the same, but
why do you start assuming that you have a population where
180 people are infected and 99800 are uninfected?
That would be a total of  , ,
and the ratio of infected to total would be
  . .
That means 1 person out of 555.5 people would be infected,
and that counts as a mistake.
You could have started with 100,000 people.
Of those,  are infected, are infected,
and the remaining  are uninfected. are uninfected.
Of the  infected people, infected people,
 will test negative. will test negative.
Of the 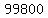 uninfected, uninfected,
 will test negative, as you said. will test negative, as you said.
The total number of people testing negative is
 . .
Comparing to that number, the number of uninfected people is
 (rounded), which could be stated as (rounded), which could be stated as 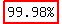 . .
NOTES:
With your calculation you should get
 (rounded), which could be stated as 99.98%. (rounded), which could be stated as 99.98%.
You mistakenly wrote your final calculation as
 (rounded), which could be stated as 99.99%. (rounded), which could be stated as 99.99%.
Neither of those numbers can be rounded to 99.9%;
they would round to 100.0% if we only give them one decimal digit.
Note that before the test,
a person knew that the probability of being uninfected was
 or 99.80%. or 99.80%.
If this virus is life-threatening (or life-altering),
people may want to know more.
If they test positive, maybe there is something they can do about it.
If they test negative,
going from 99.80% to 99.98% sure that they are safe may be cause for celebration.
|
|
|