On your TI-83 or TI-84
normalcdf(97,125,100,11), read .595947231, Press ENTER
To find "normalcdf(" on your calculator, press 2ND then 2
If your teacher won't allow calculator work, find z-scores
for the endpoints:
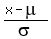
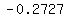and 
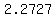If your table contains negative z values, look up z=-0.27
(the closest you can get to -.2727, and read 0.3936, and
look up z=2.27, (the closest you can get to 2.2727 and read
0.9884.
Subtract and get 0.9884-0.3936 = 0.5948.
If your table contains only positive z values, look up z=0.27
(the closest you can get to .2727, and read 0.1064, and look
up z=2.27, (the closest you can get to 2.2727 and read 0.4884.
Add and get 0.1064+0.4884 = 0.5948.
The calculator value 0.595947231 is more accurate, since we
don't have to round off the z-scores when we use the
calculator.
[It's a shame that teachers and books still require old-fashioned
inaccurate tables when technology is available so freely.]
Edwin
