Question 1061806: Identify the focus, directrix, and axis of symmetry of the parabola 6x2+3y=06x2+3y=0.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I believe the equation you tried to write is  . .
 <--> <--> <--> <--> <--> <--> . .
THE EXPECTED APPROACH:
You have memorized a few "facts" and "formulas," including the ones listed below.
1) If the equation can be written in the form 
for some real numbers  , ,  , and , and  , with , with 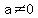 , ,
it is the equation of a parabola whose axis of symmetry is the "vertical" line  (parallel to the y-axis), (parallel to the y-axis),
and  is the x-coordinate of the vertex of the parabola. is the x-coordinate of the vertex of the parabola.
2) For a parabola with a "vertical" axis of symmetry,
you can find the y-coordinate,  , of the vertex of the parabola, , of the vertex of the parabola,
by substituting 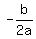 for for  in the equation of the parabola. in the equation of the parabola.
3) For a parabola with a "vertical" axis of symmetry,
if  , and , and  is the coordinate of the vertex, is the coordinate of the vertex,
the coordinates of the focus are
 , ,
and the directrix is the line  . .
Applying that to  , we have , we have  , ,  , ,
 . .
So ,  is the axis of symmetry and the x-coordinate of the vertex. is the axis of symmetry and the x-coordinate of the vertex.
The y-coordinate of the vertex is  . .

The coordinates of the focus are  , ,
and the equation of the directrix is  . .
THE NON-MEMORIZER APPROACH:
You realize that is  shows x as an even function of x shows x as an even function of x
(one that assigns the same y value to any pair of opposite values of x,  and and  ), ),
meaning that the y-axis,  , is the axis of symmetry. , is the axis of symmetry.
You realize that  , making (0,0) a maximum and the vertex of the parabola. , making (0,0) a maximum and the vertex of the parabola.
That also tells you that the focus is a the focal distance  below the vertex at below the vertex at  , ,
and that the directrix is the horizontal line  , ,
both at the same distance from the vertex, and on opposite sides of the vertex.
You may remember that  , ,
or you may use the definition of parabola to find  . .
All points is a parabola are at the same distance from focus and directrix.
The point with  , at a distance , at a distance  from the focus, from the focus,
has the y-coordinate  . .
Its distance to directrix  is is
 --> --> --> --> --> --> --> --> --> -->
|
|
|