SOLUTION: Please help me solve this equation: find the inverse of the function {{{f(x)=x^2+1/2}}}

Algebra ->  Inverses -> SOLUTION: Please help me solve this equation: find the inverse of the function {{{f(x)=x^2+1/2}}}      Log On


   

Question 1061793: Please help me solve this equation: find the inverse of the function
f%28x%29=x%5E2%2B1%2F2
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
With the function f%28x%29 as written,
there is an inverse relation (not an inverse function),
y+=%22+%22+%2B-+sqrt%28%282x-1%29%2F2%29 ,
that can be found from y=x%5E2%2B1%2F2
by interchanging x and y ,
and then "solving for y."
If we define the function with a restricted domain, as
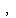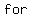f%28x%29=x%5E2%2B1+%2F+2%22+%2C%22%22for%22x%3E=0%29 ,
then it has an inverse function, which is
f%5E%28-1%29%28x%29=sqrt%28%282x-1%29%2F2%29 or f%5E%28-1%29%28x%29=sqrt%28x-1%2F2%29 .
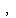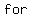When we interchange x and y from y=x%5E2%2B1%2F2%22+%2C%22%22for%22x%3E=0%29 ,
we get
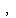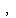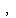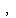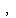x=y%5E2%2B1%2F2%22+%2C%22%22with%22y%3E=0%29 ,
x=%282y%5E2%2B1%29%2F2%22+%2C%22%22with%22y%3E=0%29 ,
2x=2y%5E2%2B1%22+%2C%22%22with%22y%3E=0%29 ,
2x-1=2y%5E2%22+%2C%22%22with%22y%3E=0%29 ,
%282x-1%29%2F2=y%5E2%22+%2C%22%22with%22y%3E=0%29 , and
y=sqrt%28%282x-1%29%2F2%29 <--> y=sqrt%28x-1%2F2%29 .