|
Question 1061433: A movie theater holds 1000 people. With the ticket price at $8 during the week, the attendance at the theater has been 200 people. A market survey indicates that for every dollar the ticket price is lowered, attendance increases by 50.
(a) Find a function that models the revenue R in terms of the ticket price x .
(b) What ticket price will maximize the revenue?
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website! .
A movie theater holds 1000 people. With the ticket price at $8 during the week, the attendance at the theater has been 200 people.
A market survey indicates that for every dollar the ticket price is lowered, attendance increases by 50.
(a) Find a function that models the revenue R in terms of the ticket price x .
(b) What ticket price will maximize the revenue?
~~~~~~~~~~~~~~~~~~~~~~~~
If to translate the condition in the Math language, it means:
With the ticket price changing according to the function P = 8-z dollars the attendance changes as N = 200 + 50z people.
Express the revenue as function of z and find its maximum.
Notice that my variable "z" relates to the variable "x" of the original condition as z = 8-x, or x = 8-z.
But my reformulation is actually in the precise accordance with the first part of the condition and is more understandable.
To solve the problem, you must know that the revenue is the product P*N, i.e.
Revenue R = (8-z)*(200+50z).
Or, which is the same,
R = 1600 - 200z + 400z - 50z^2, or
R =  . (1)
Now, let me remind you that for general quadratic function f(x) =  the minimum/maximum is at x =  .
In your case the maximum is at z = 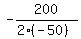 =  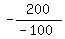= 2.
It means that the optimal price of the tickets is P = 8-2 = 6 dollars.
The maximum revenue is the value of the quadratic function (1) at z = 2"
R =  = -200 + 400 + 1600 = 1800 dollars.
Answer. The revenue is maximal $1800 at the ticket price $6.
(The attendance then is 200 + 50*2 = 300 and (for the check purpose) $6*300 = $1800).
Solved.
On finding the maximum/minimum of a quadratic function see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
- A rectangle with a given perimeter which has the maximal area is a square
- A farmer planning to fence a rectangular garden to enclose the maximal area
- A farmer planning to fence a rectangular area along the river to enclose the maximal area
- A rancher planning to fence two adjacent rectangular corrals to enclose the maximal area
in this site.
Also, you have this free of charge online textbook in ALGEBRA-I in this site
- ALGEBRA-I - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this textbook under the topic "Finding minimum/maximum of quadratic functions".
|
|
|
| |
