SOLUTION: If f(x) = (x-3) logx, then prove the equation xlogx = 3-x is satisfied by at least one value of x lying between 1 and 3.

Algebra ->  Logarithm Solvers, Trainers and Word Problems -> SOLUTION: If f(x) = (x-3) logx, then prove the equation xlogx = 3-x is satisfied by at least one value of x lying between 1 and 3.      Log On


   

Question 1061353: If f(x) = (x-3) logx, then prove the equation xlogx = 3-x is satisfied by at least one value of x lying between 1 and 3.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
This problem might as well be stated:

"If the capital of Georgia is Atlanta, then prove the equation 
xlogx = 3-x is satisfied by at least one value of x lying 
between 1 and 3."

That's because "f(x) = (x-3)logx" has no more to do with whether

"the equation xlogx = 3-x is satisfied by at least one value of x 
lying between 1 and 3" than the capital of Georgia being Atlanta 
has to do with it!

Thus we ignore the f(x) part and take the problem to be:

Prove that the equation 

x%2Alog%28%28x%29%29+=+3-x 

is satisfied by at least one value of x lying between 1 and 3.

Consider the function which is continuous on [1,3]

g%28x%29=x%2Alog%28%28x%29%29-3%2Bx

g%281%29=1%2Alog%28%281%29%29-3%2B1=-2

g%283%29=3%2Alog%28%283%29%29-3%2B3=1.4313638...

g(1) is negative and g(3) is positive.

Thus there is some number, say h, on [1,3] such that

g%28h%29=0

Thus

g%28h%29=h%2Alog%28%28h%29%29-3%2Bh=0

and

h%2Alog%28%28h%29%29+=+3-h

[Note: If you require that h be an algebraic number then
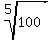choose h to be root%285%2C100%29]

Edwin